2021年度 令和3年度 神奈川県 公立高校入試問題 数学 過去問の解説です。令和3年度 共通選抜 学力検査問題 全日制 数学。
神奈川県 公立高校入試 2021年 数学 過去問 解説 問1
問1。(ア)から(オ)まで


問1 ア)
負の数が引き算されるときは 符号が反転し +になる。
イ)
12で分母を通分して計算。
ウ)
かけ算と割り算を ひとつの大きな分数に表し まとめて約分していくと 計算が楽。

エ)
分母を15に通分する。分子の足し算引き算の符号に注意する。
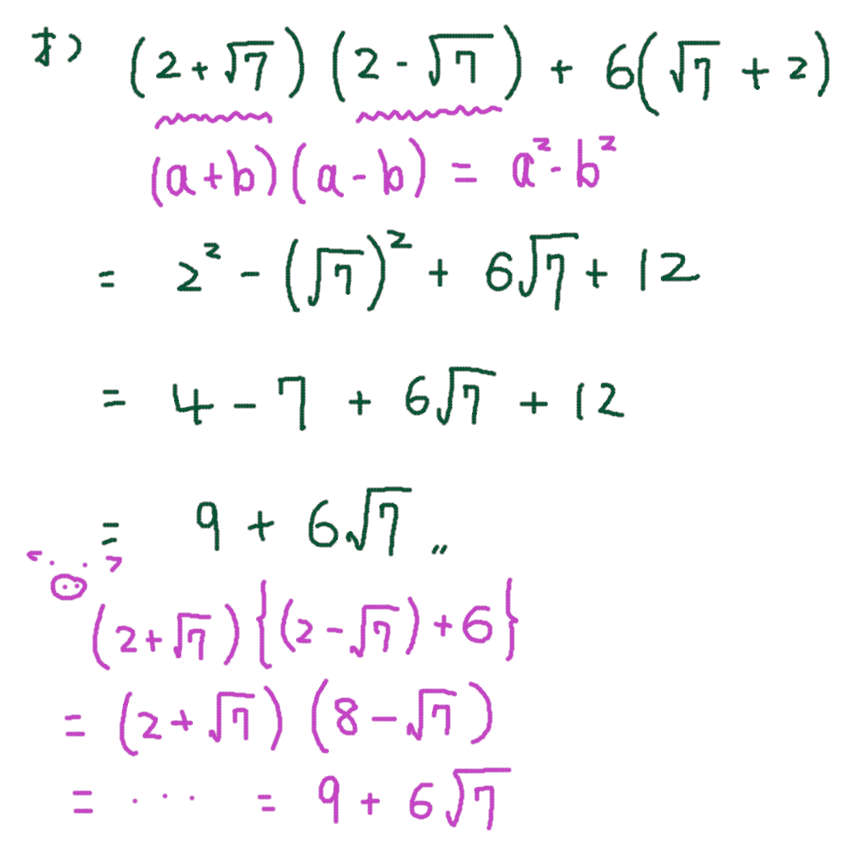
オ)
共通因数でまとめたくなるが、そのまま計算したほうが速い。
神奈川県 公立高校入試 2021年 数学 過去問 解説 問2
問2。(ア)から(カ)まで


問2 ア)
x+6をAとおいて因数分解。Aを元に戻す操作を忘れないように。
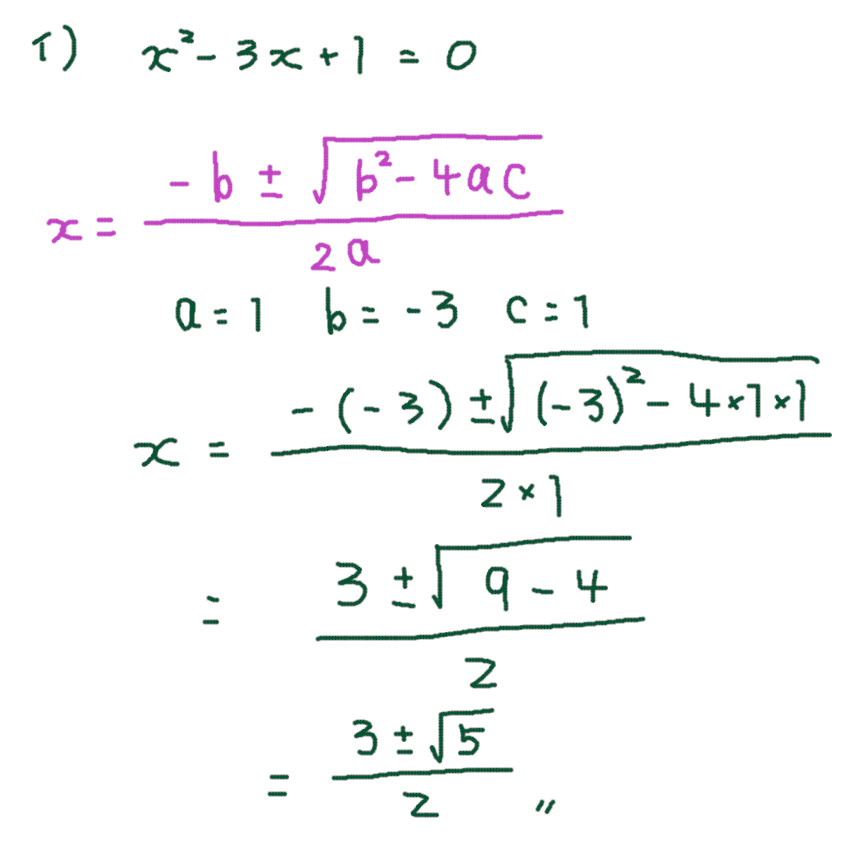
イ)
因数分解できないので、平方完成か解の公式を使う。解の公式が楽ちん。
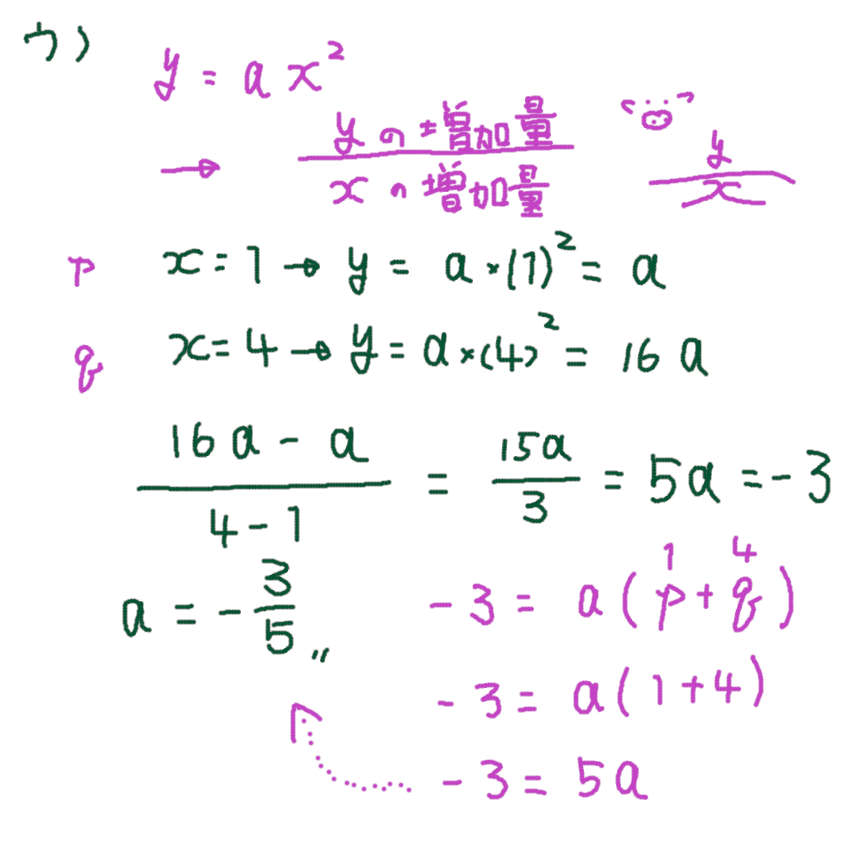
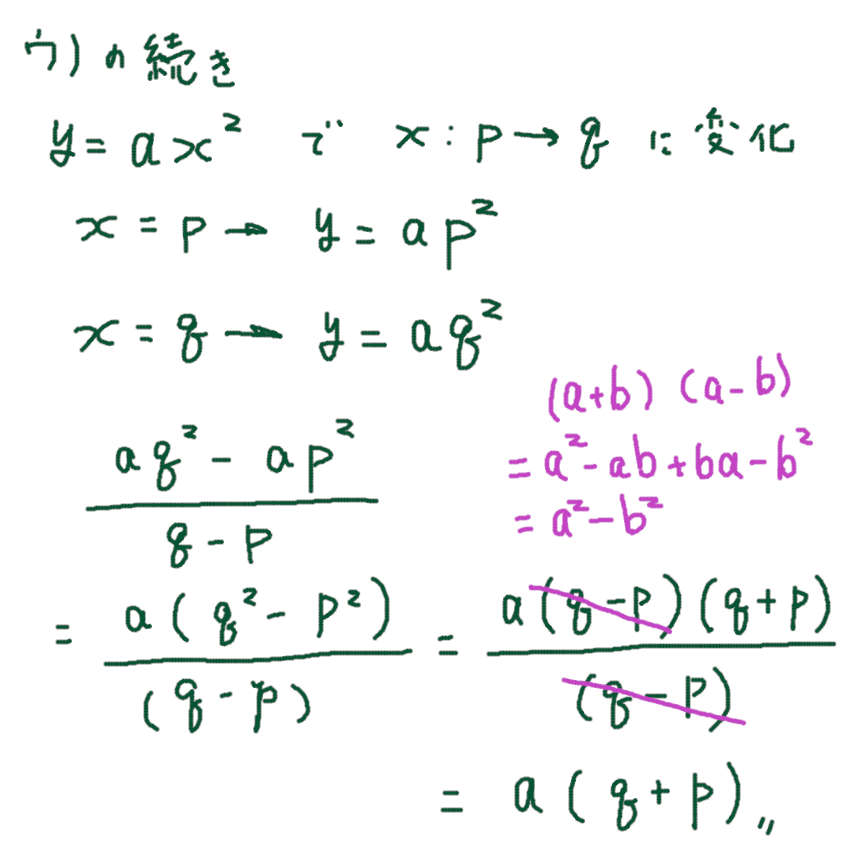
ウ)
変化の割合は xの増加量と yの増加量を 比べたもの。変化の割合 = a(q+p)を知っていると有利。


エ)
以上なので200kgも含まれるから=も必要。
オ)
自然数の定義は1,2,3,4...となる。540を素因数分解して、平方根の中身が平方数になるようにnを求める。
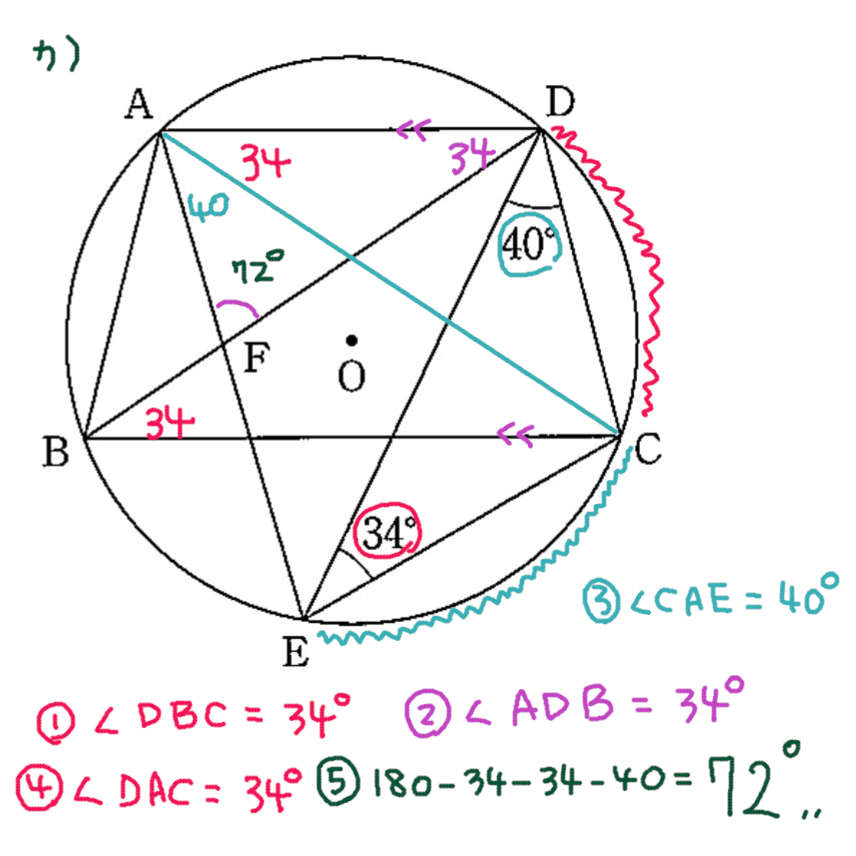
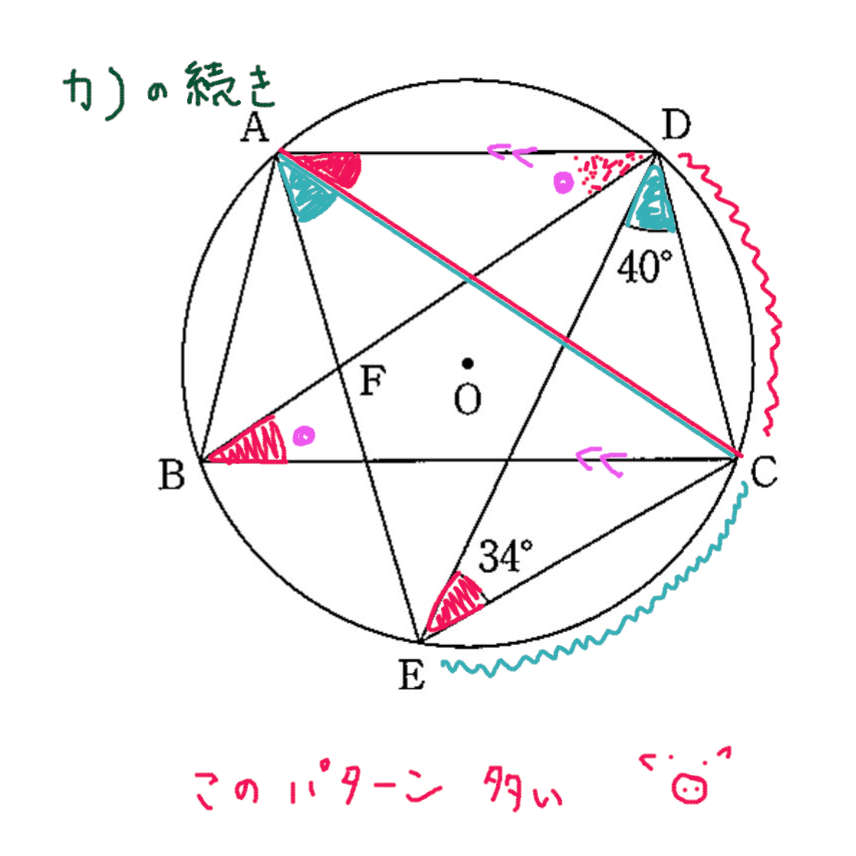
カ)
円周角の定理と錯角と 補助線を1本引いて解く。このパターンの問題も多い気がする。
問1が各3点。問2が各4点。ここまでで 39点の配点。過去問を見ると 毎年同じような似たような問題が出題されている。ので、集中して練習すれば 満点が狙えると思う。
神奈川県 公立高校入試 2021年 数学 過去問 解説 問3
問3。(ア)から(エ)まで。
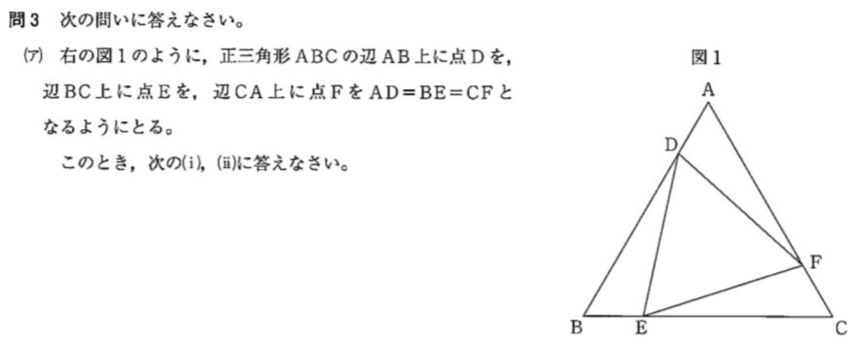

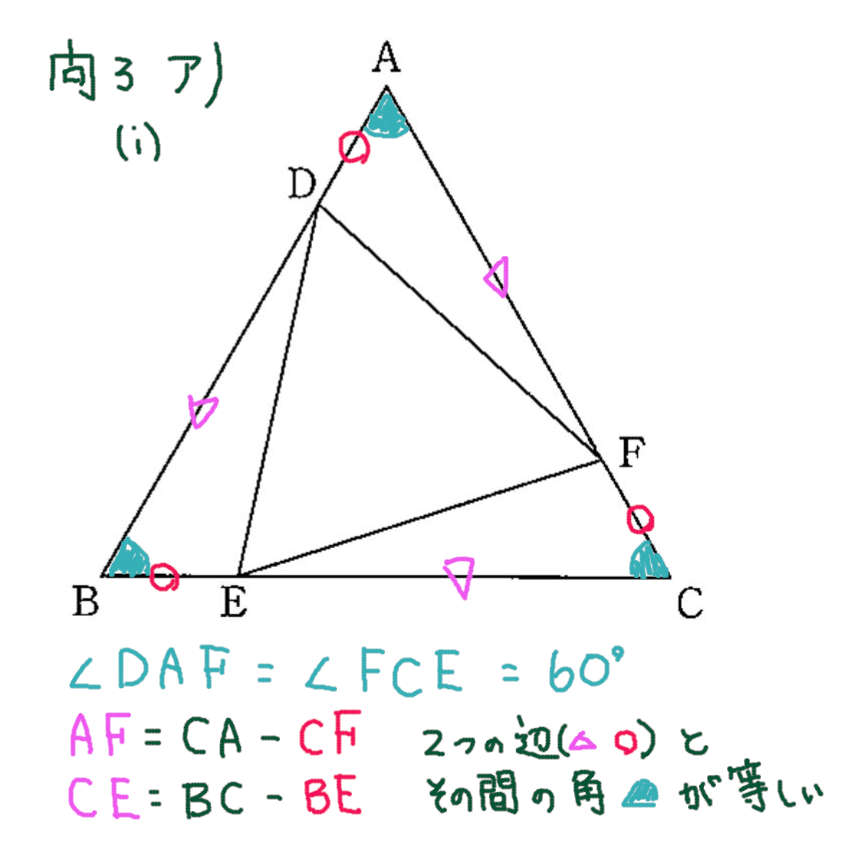
問3 ア)(i)
正三角形はすべての辺の長さが等しい。正三角形はすべての角の大きさが等しい。2組の辺の長さと その2組の辺に はさまれた角の大きさが それぞれ等しい 三角形は合同。
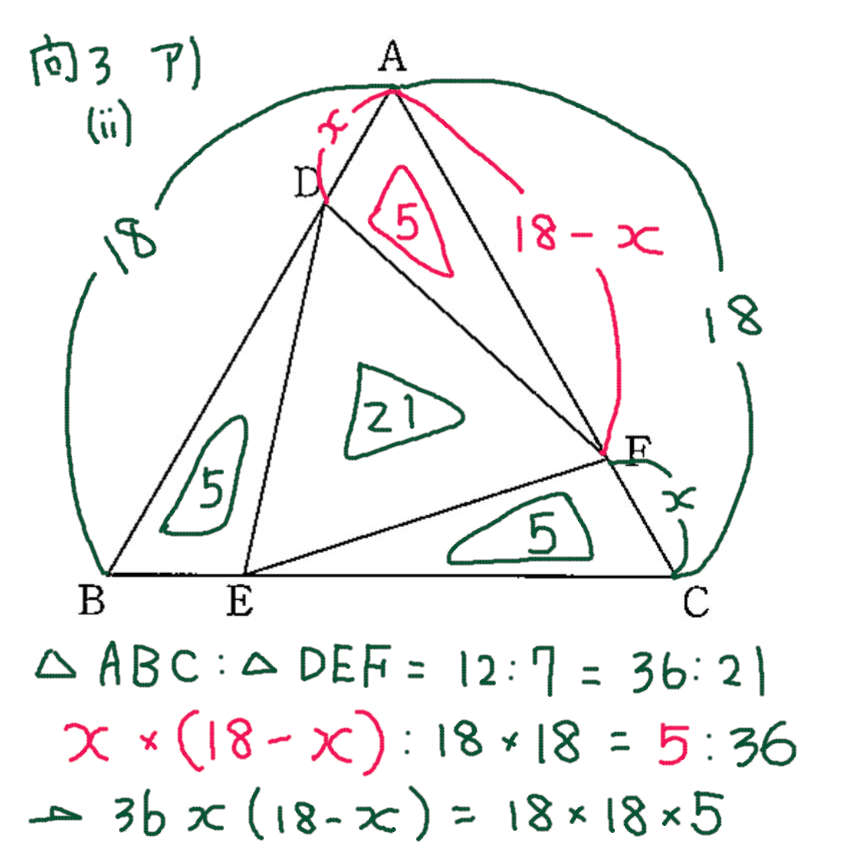

ア)(ii)
ひとつの角が等しい三角形の 面積比と辺の比 の関係を使って解く とそんなに難解ではない気がする。けれど、アプローチを失敗すると難問になってしまう。
条件としてあたえられる12:7という面積比を 3倍して36:21にしておくと、計算が簡単。
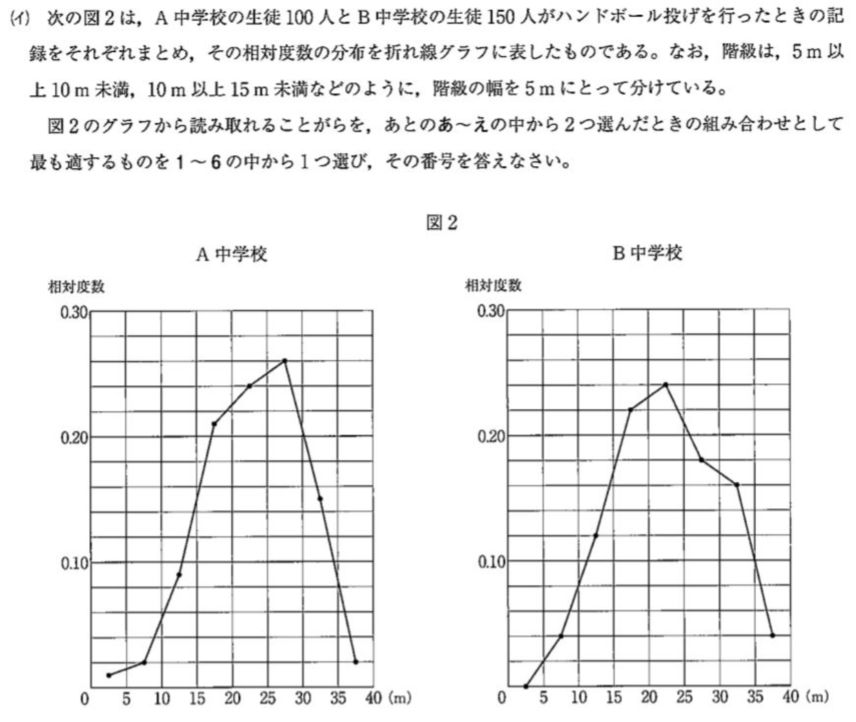

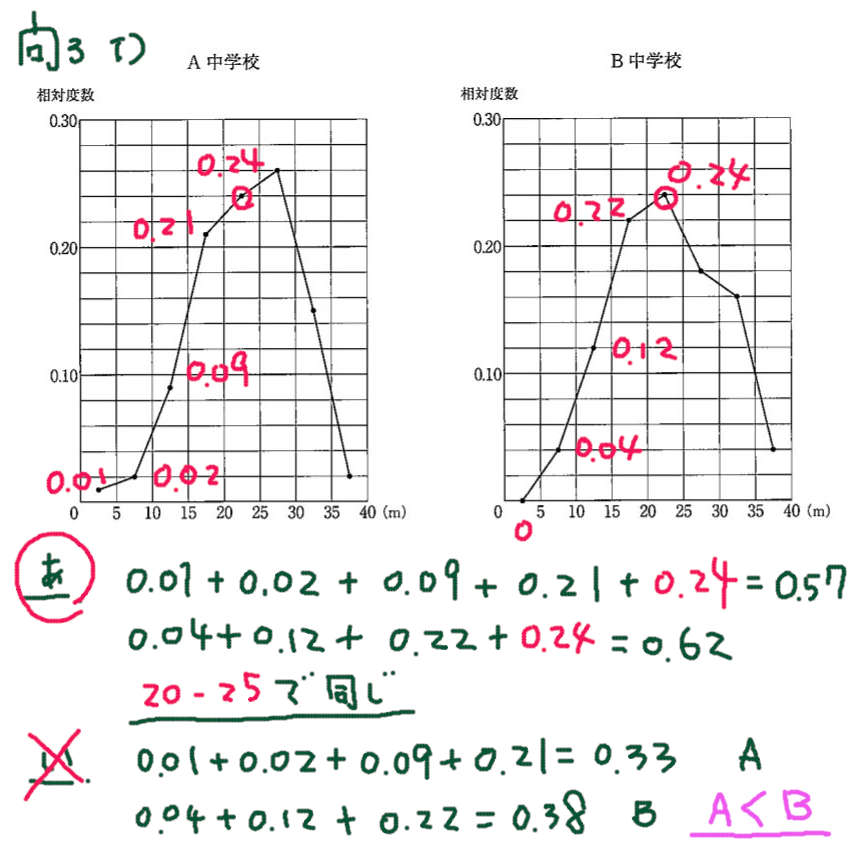
あ)
相対度数になっていて 中央値なので 0.5を超えるまで足し算をして 超えた階級に中央値が含まれる。
い)
割合を問われているので、20未満の階級をすべて足し算。
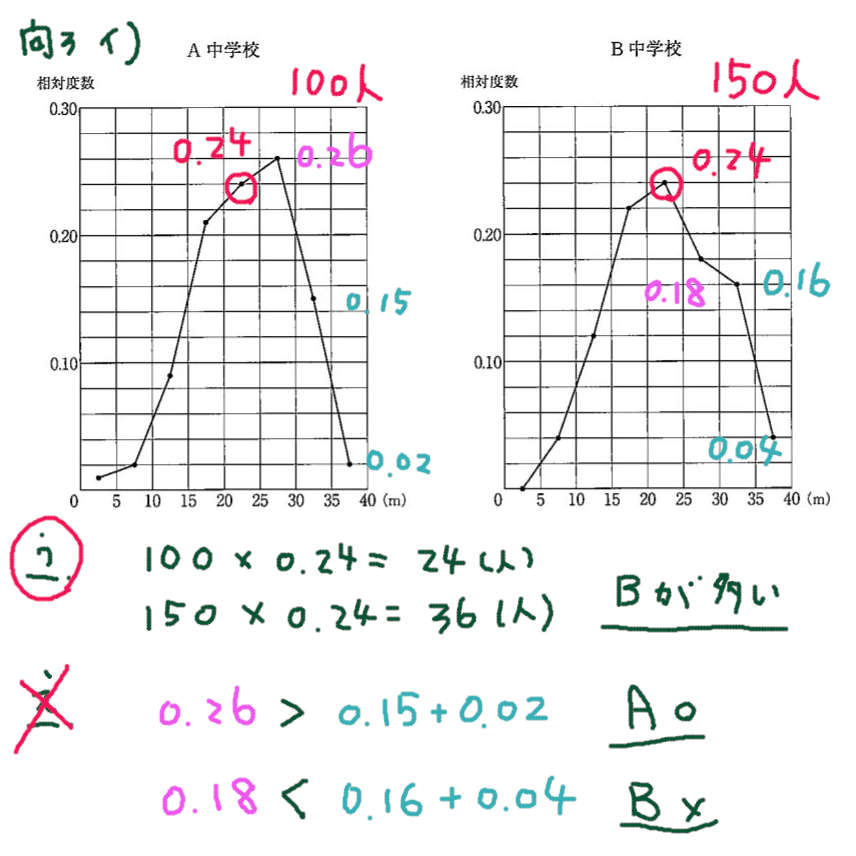
う)
具体的な人数を問われている。相対度数は合計人数で割った値なので、それぞれの相対度数に合計人数をかけて人数に変換する。
え)
AとBのそれぞれの事象に対して 問われているので、AとBの相対度数でそのまま計算して大丈夫。
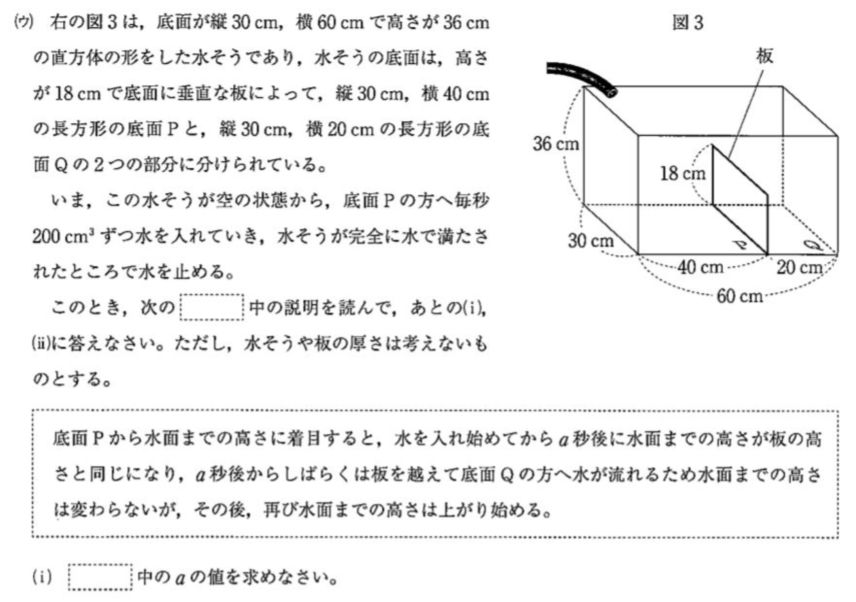
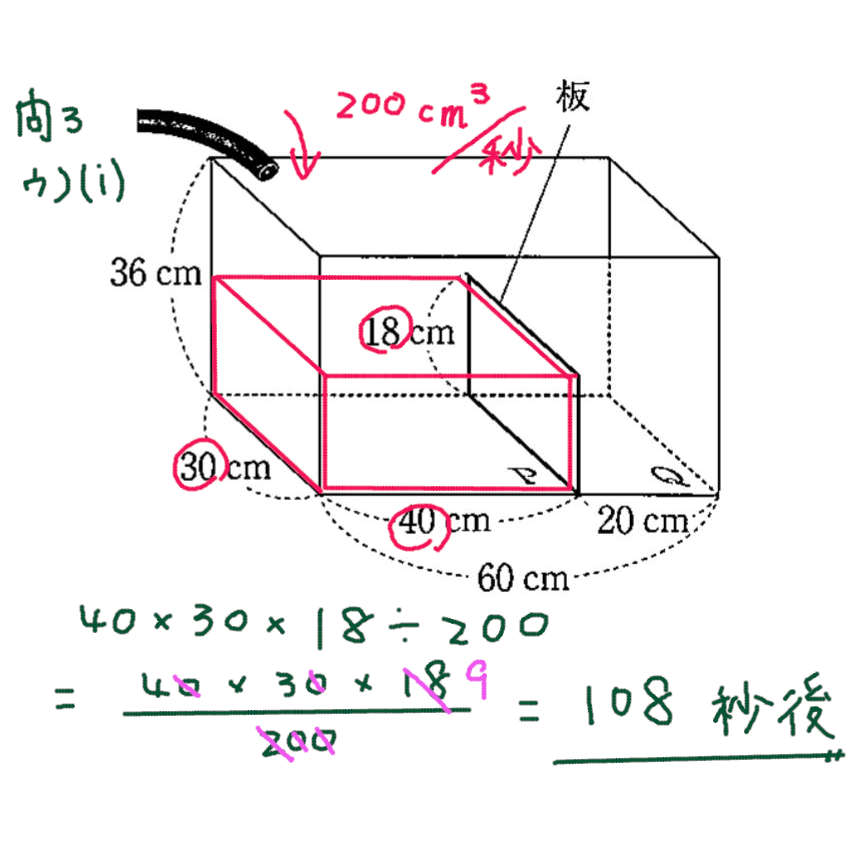
ウ)(i)
板の高さを超えるまでは 底面P側だけに 水がたまる。

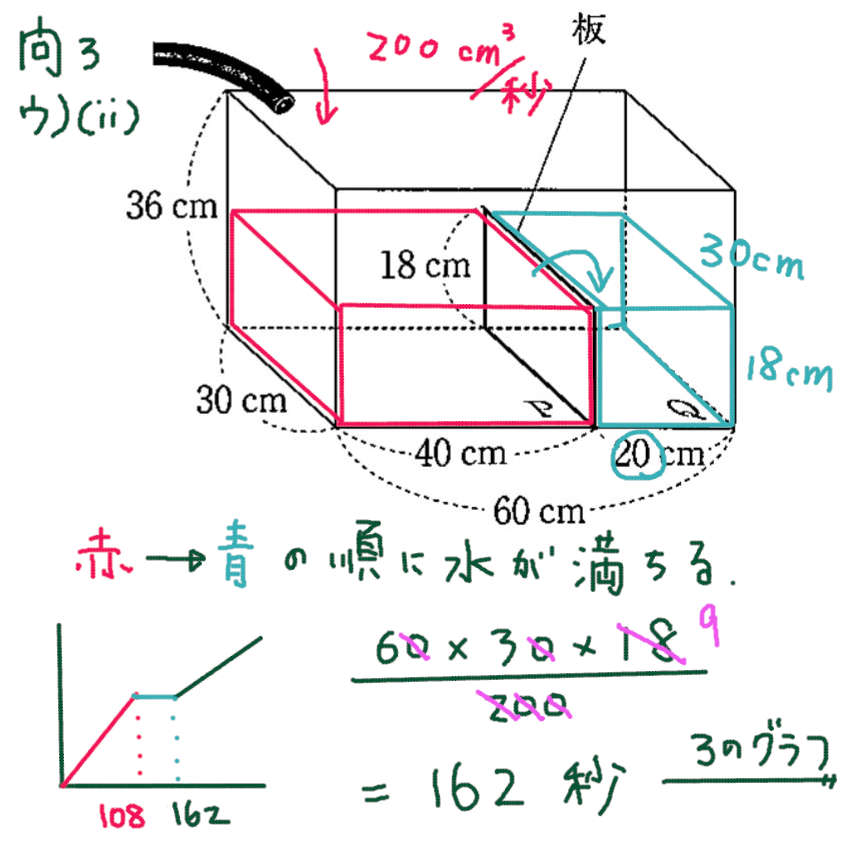
ウ)(ii)
赤⇒青 の順番で 水が満ちる。青(底面Q)側に水がたまるとき 水面の高さは変化しない。


エ)
1割 3割 などを小数を使ったかけ算の形で表せるのかどうか。連立方程式が解けるのかどうか。文章で問われていることを 数式に置き換える作業は 意外と難しい?
神奈川県 公立高校入試 2021年 数学 過去問 解説 問4
問4。(ア)から(ウ)まで。
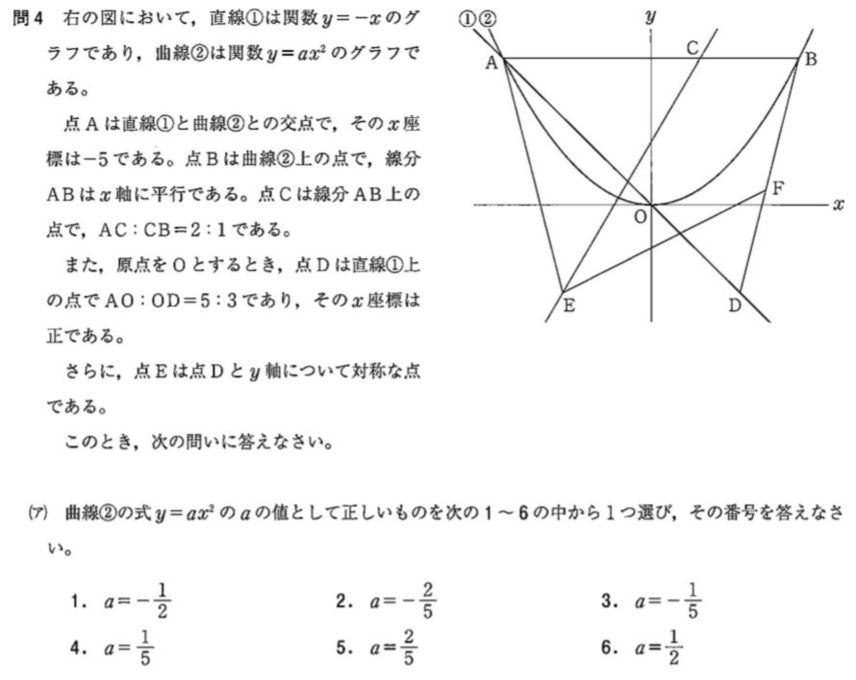
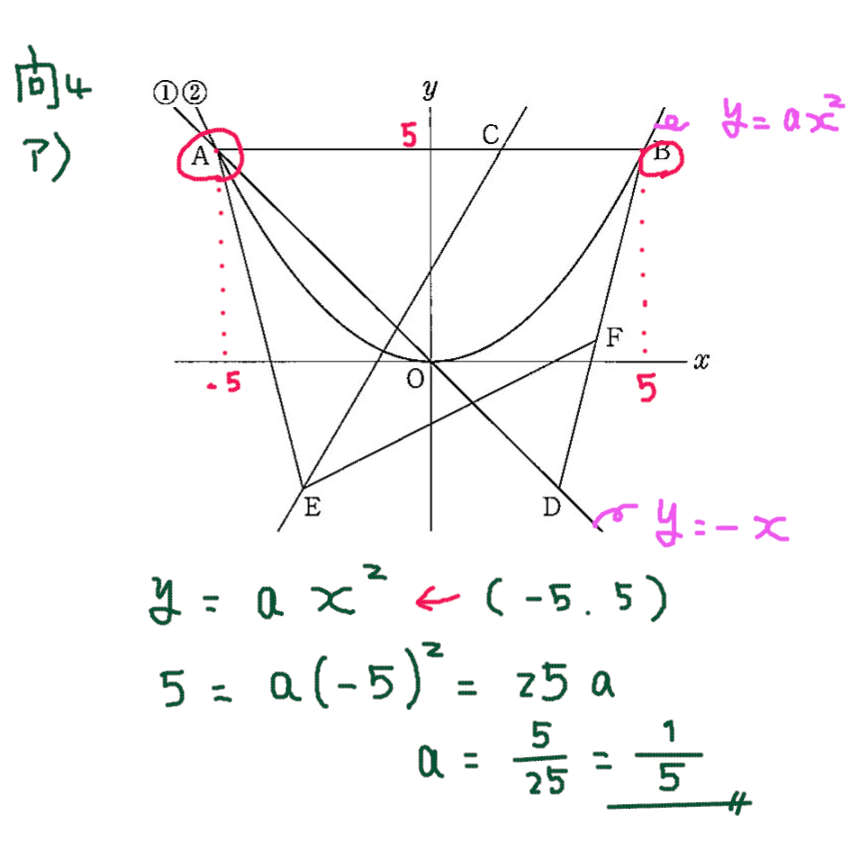
問4 ア)
試験後半の問題になっても ア)の問題は 簡単?なことが多いので、先に取り組むと得点につながる。落ち着いて問題文の条件を グラフに書き込むと よい。

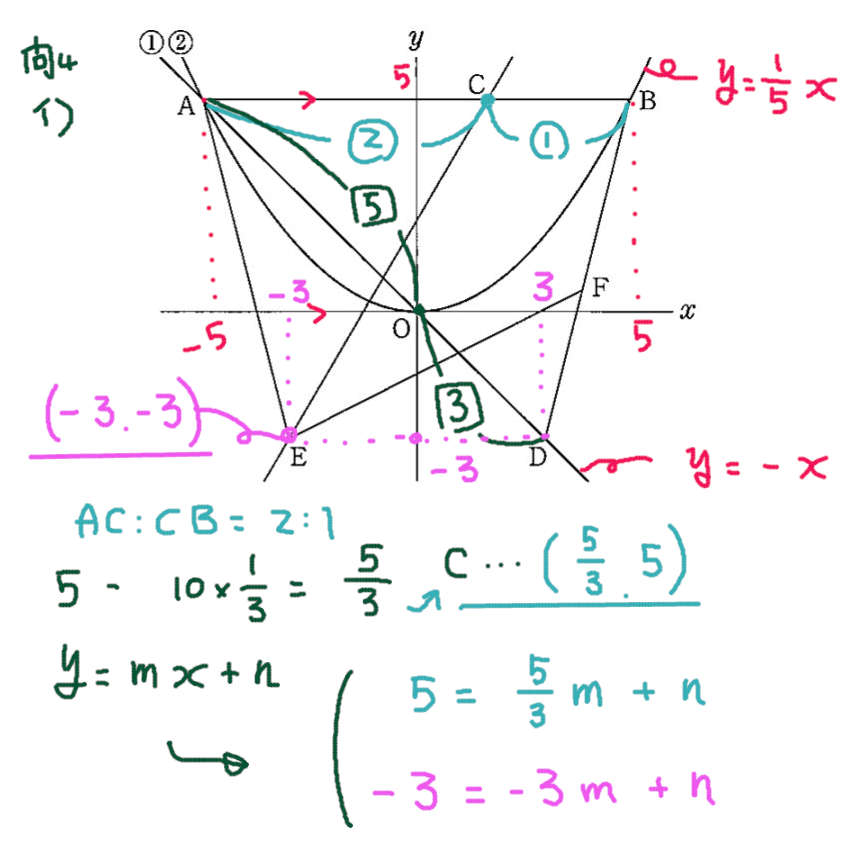
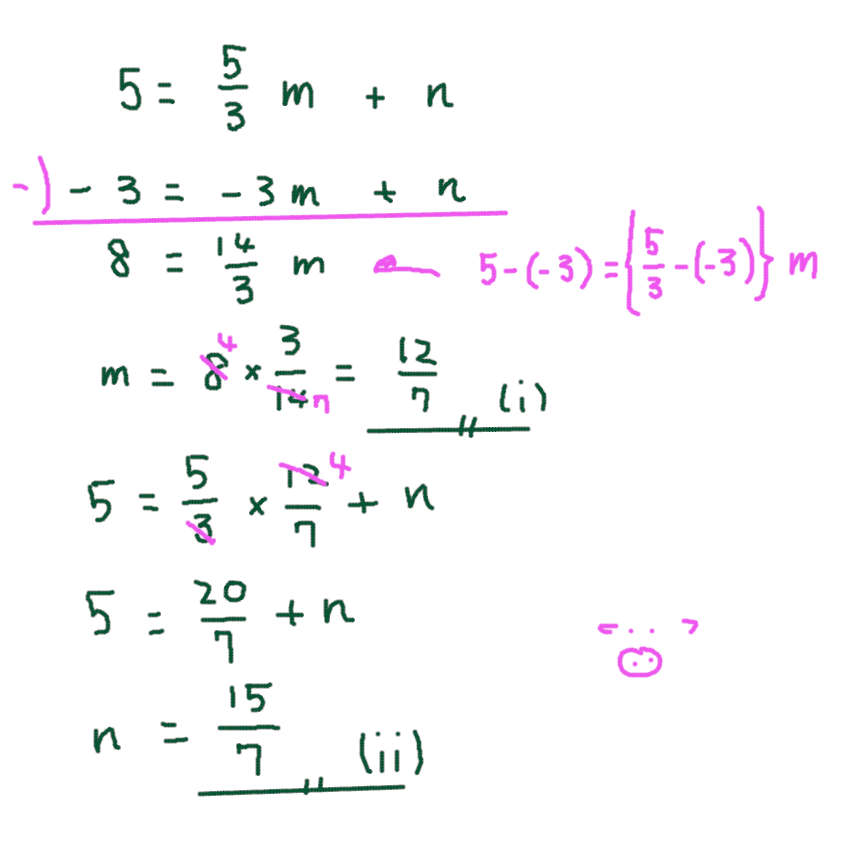
イ)
CとEの座標を求めてから、連立方程式を解く。分数になってしまうので、悲しい計算間違いを 起こさないように注意。
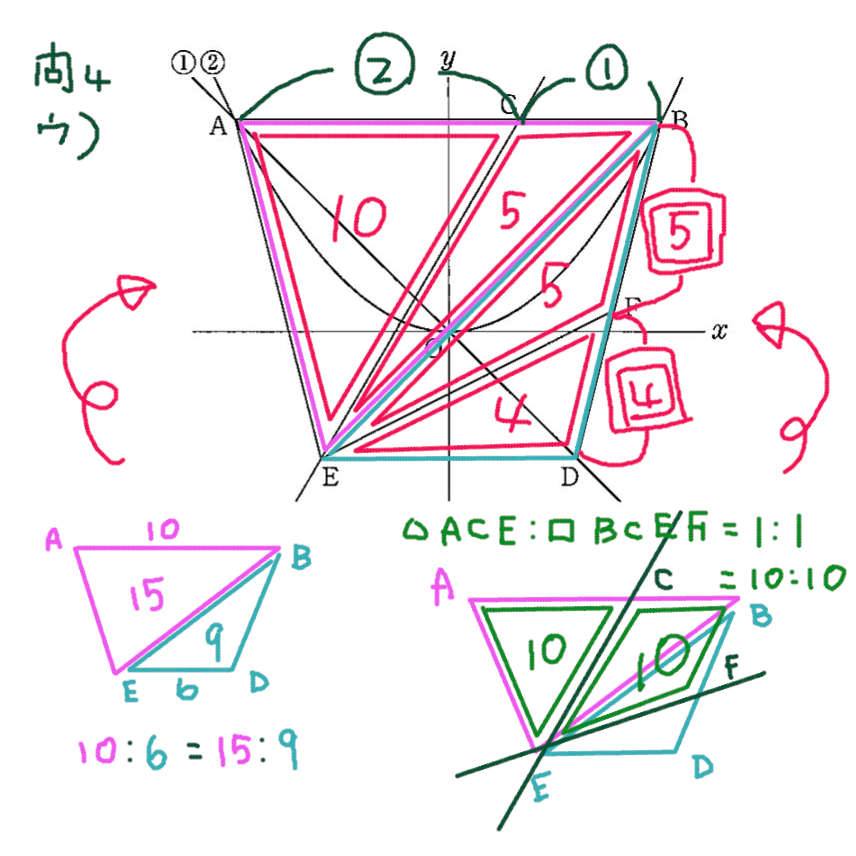
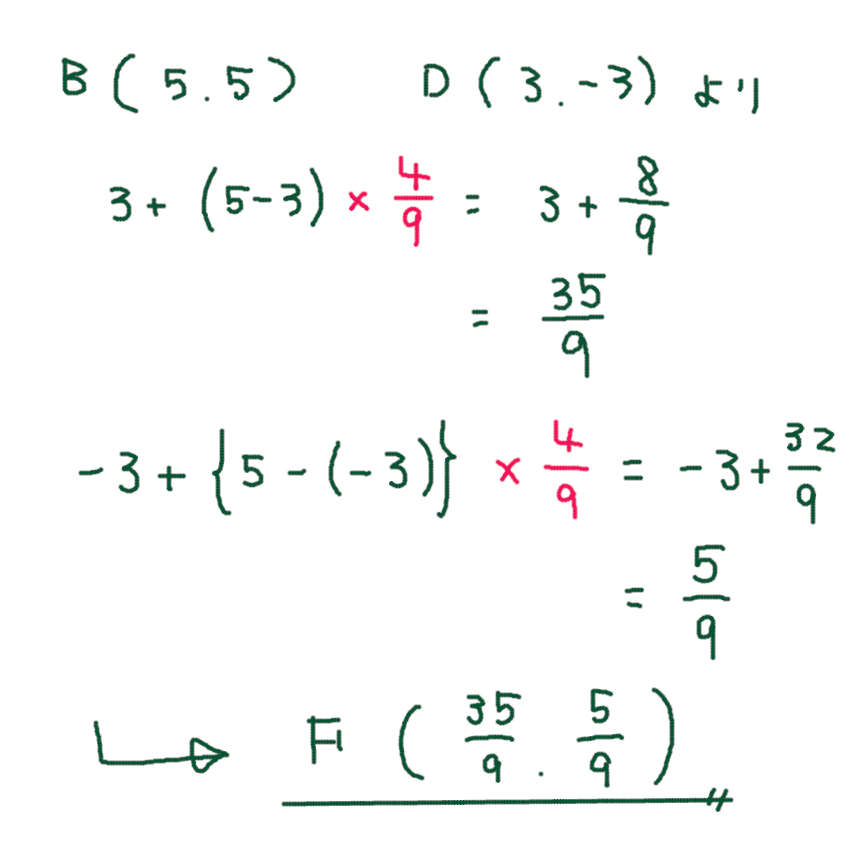
ウ)
高さが等しい三角形の面積比は 底辺の長さの比になる ことを利用する。パターンといえばパターンだが、ひらめくまでに 時間がかかる場合も多いので、ひととおり簡単にできる問題を終わらせてから取り組むべき。
神奈川県 公立高校入試 2021年 数学 過去問 解説 問5
問5。(ア)から(イ)まで。
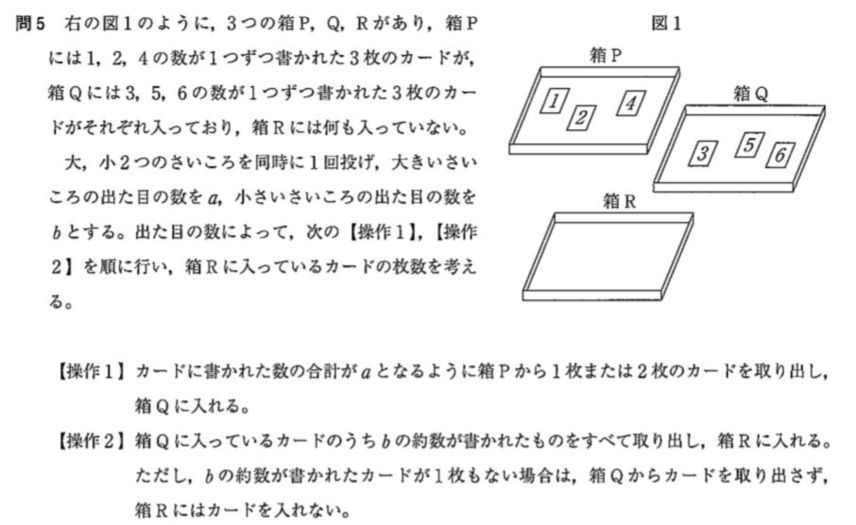
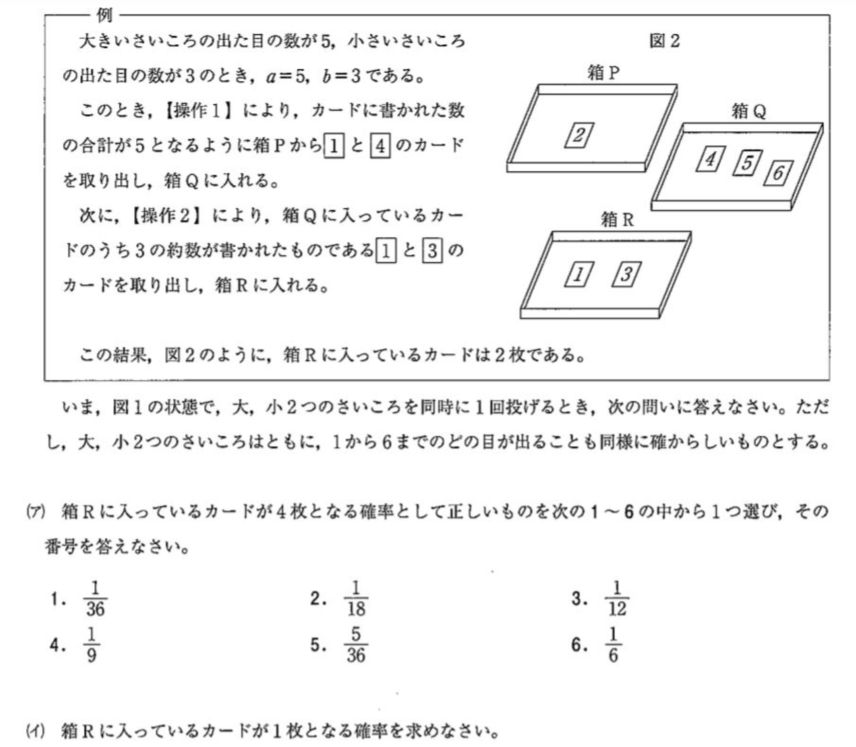

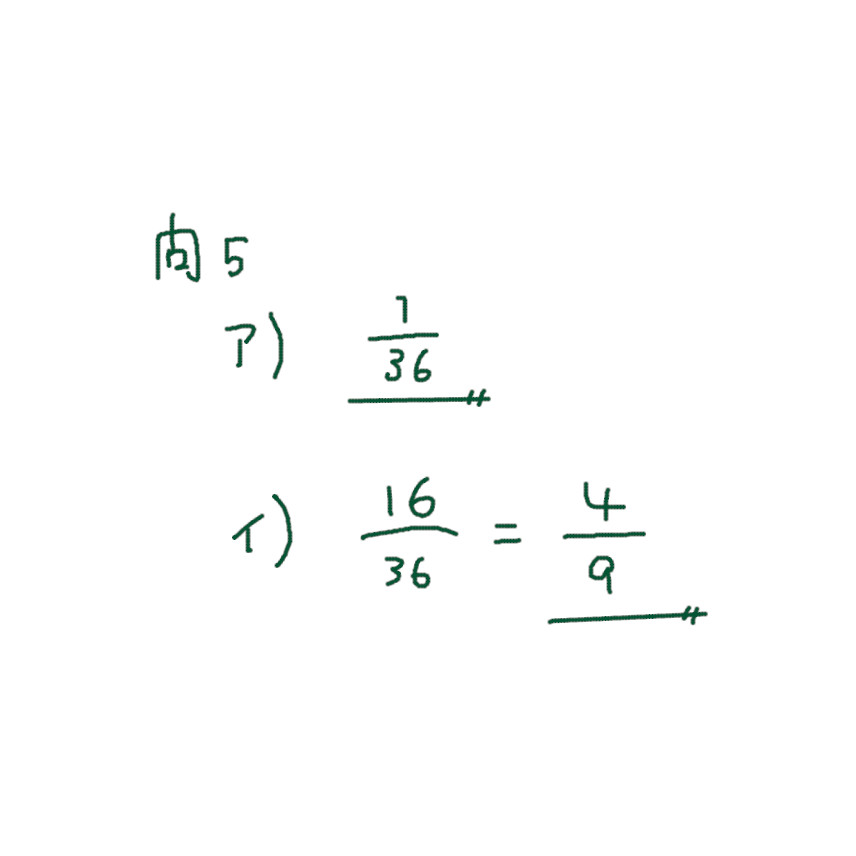
問5 ア)イ)
神奈川県 高校入試問題 数学は 大小2つのさいころを転がす問題が大好き。なので、6×6=36通りしかパターンは存在しない。ということは、全部のパターンを表にして書き出すべき。
ちょっと面倒に感じるかもしれないが、じっくり問題分を読んで、状況を表に整理すれば、絶対に解ける。全部のパターンを書けば うっかり数え損ねることもない。
全部を表に書き出さないで スマートに解こうとするよりも、速く解けると思う。
神奈川県 公立高校入試 2021年 数学 過去問 解説 問6
問6。(ア)から(ウ)まで。

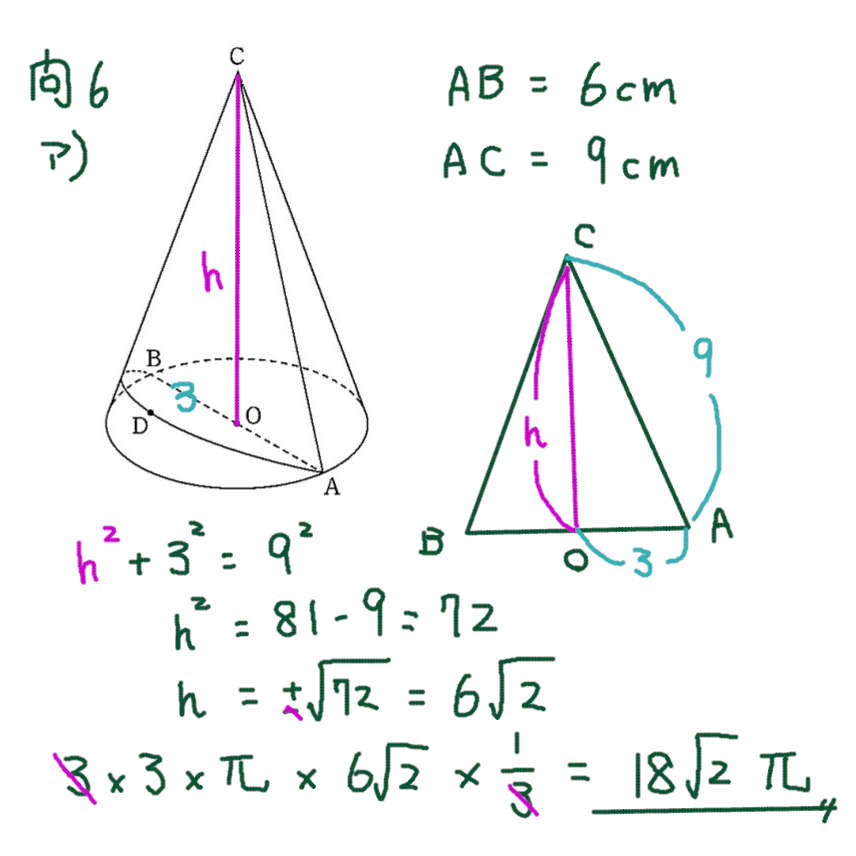
問6 ア)
円すいの高さを三平方の定理で求める。
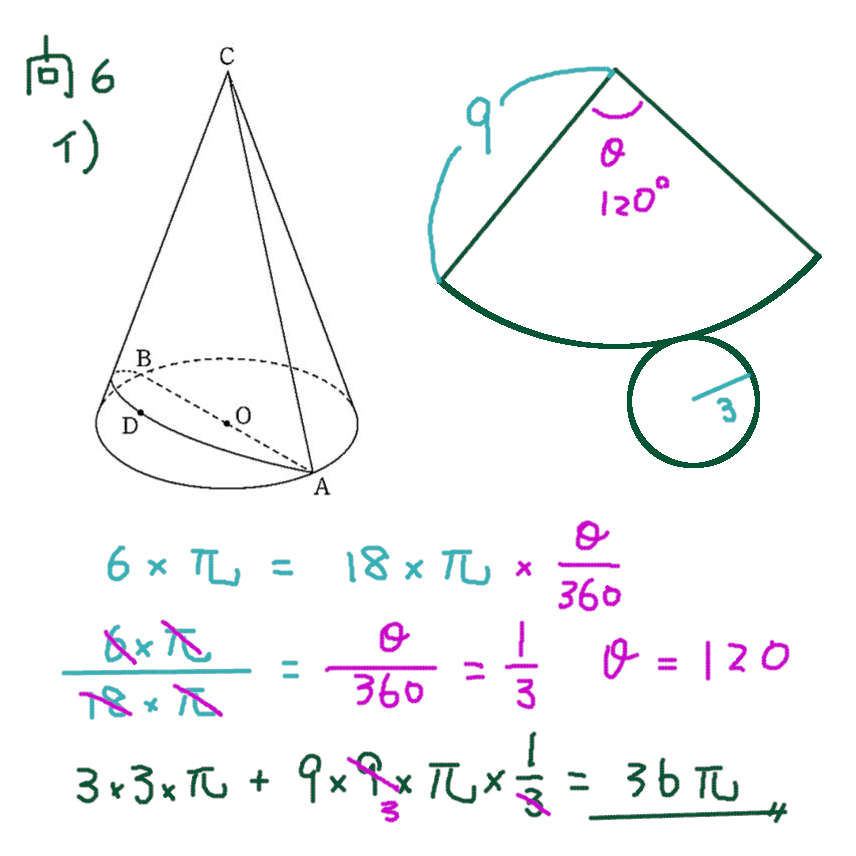
イ)
円すいの側面を展開して できる扇形の中心角を求めたくなるが、途中まで計算した状態で先に進むと そのあとの計算が楽。

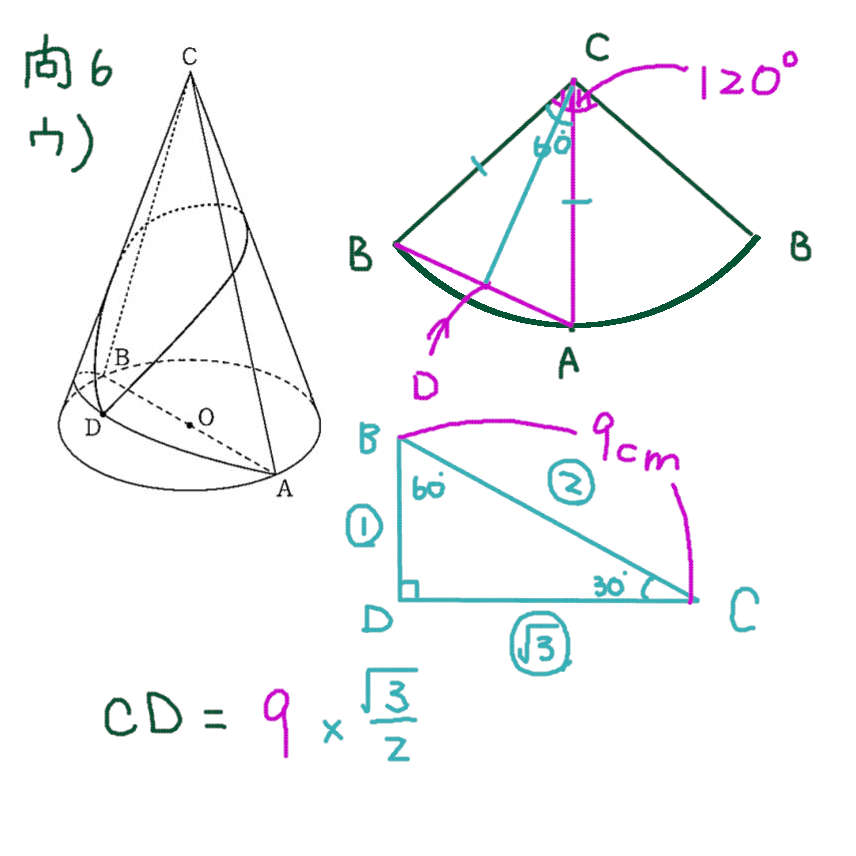
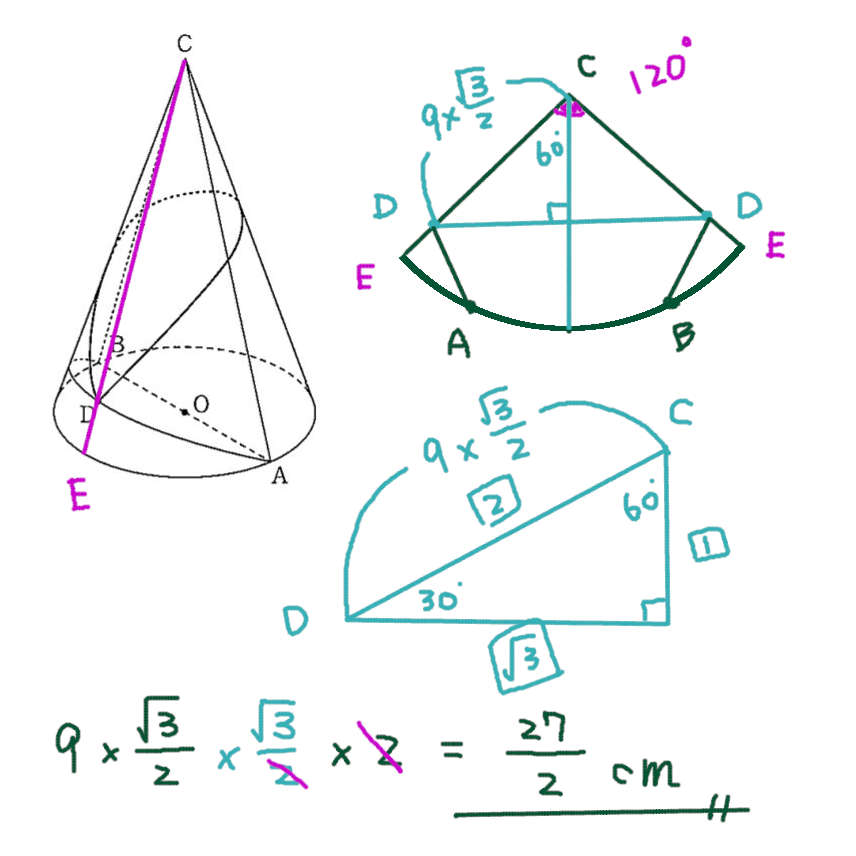
ウ)
最も短くなるように引いた線(最短距離)の問題は、展開図を調べる ⇒ 三平方の定理や相似を使って解く流れが多い。
問6 ウ)は、展開図を切り開く位置を変えて 2回展開図を書くと、状況を整理しやすい。
解く順番の攻略
ここが一番大事。
「本当は解けたのに 時間がなかったから 手がつけられなかった」⇒ これが一番モッタイナイ。
問2 カ)4点
問3 ア)の( ii)4点
問4 ウ)5点
問6 ウ)5点
これらは、正答にたどり着くまでに時間がかかる もしくは 気がつかないとできない(知っていればできる)系の問題。なので、30秒考えて「分からんかも」と感じたら、どんどん先に進むべき。
例えば 問6 ア)イ)は 練習すれば 簡単に解ける。こっちを得点するべき。
上記問題以外を正答すれば82点得点。平均点は58点。中央値が含まれたのは51点-60点。
上記問題以外を正答して 82点は絶対に得点したい。さらに上記問題の中で 1問でも多く正答できれば、志望校の合格に近づく。
解き方を知っていればできる系の問題を 確実に正答するために、過去問を繰り返し練習するべき。

2020年 令和2年 神奈川県 高校入試 数学 過去問 解説 ⇒ 2020年度 神奈川県公立高校入試問題 数学 過去問の解説