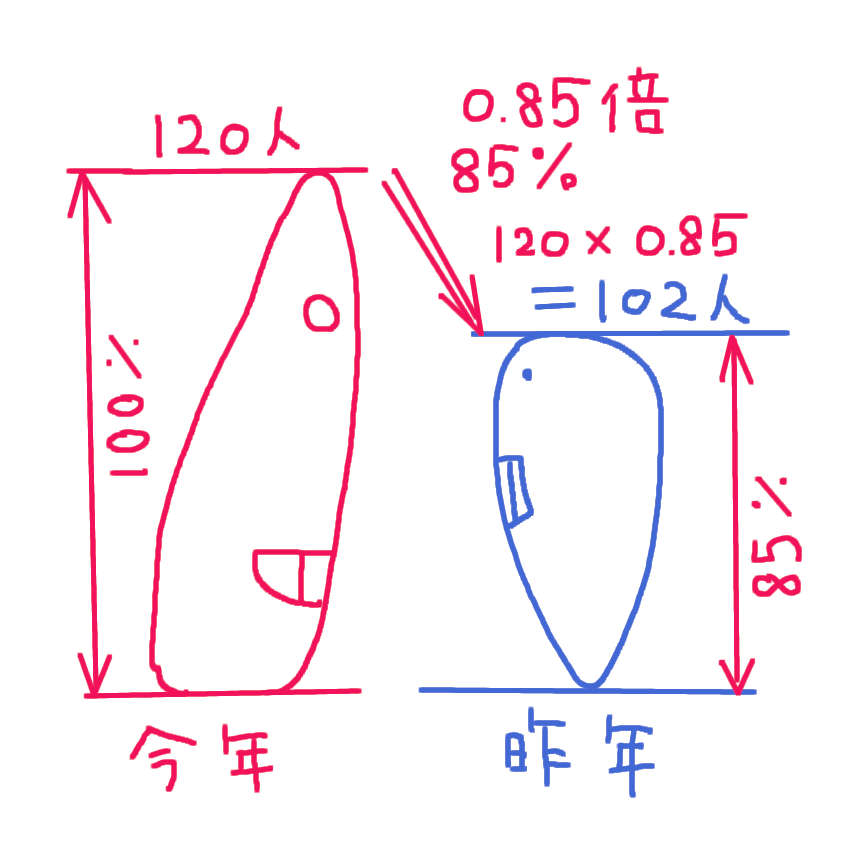
「割合」の問題は、「何倍?」と同じ(似たような)感覚で取り組むと 意外とすんなり解けるかもしれません。

果物が4コ入るカゴがあります。
8コのリンゴがあります。
リンゴの数(8コ)は カゴに入る果物の数(4コ)の 何倍ですか?

数だけを抜き取ると「8は 4の何倍ですか?」
8は 4の2倍です。
この「2倍」の「2」という数が「割合」と呼ばれる数字です。「200%」と表現されることもあります。
割合の問題は 日本語の問題だと思う ⇒ 公式を使わない 割合の問題の解き方 小学生 算数
くもわ(公式)や、比べる量 もとにする量(比べられる量 全体の量)などの難しい言葉を 使わなくても、「何倍?」を考えると 割合の問題を解くことができます。
ちょっと余談。
「何倍」という表現は、2倍 3倍のように 数が大きくなる方向のときに 使われやすい傾向があります。
一方で「割合」を表す言葉は、消費税10%や打率3割のように 数が小さくなる方向のときに 使われやすい傾向にあります。
もうちょいつっこむと 5割増しという言葉などもあるように 2倍までは増えないんだけど 1.5倍増えている ⇒ 変化した量が もともとの数よりも小さい場合の説明に 使われやすい表現です。
(もっと どうでもいいお話ですが、割合の表現方法(使いこなし?)を観察すると 理系出身かどうかが なんとなく分かってしまいます。)
もっと余談。

もうちょっと分かりやすい?と思われるページを作りました ⇒ 割合の問題は「何倍?」を考えると 解きやすい
公式を使わない割合の求め方
果物が8コ入るカゴがあります。
5コのリンゴがあります。

リンゴの数(5コ)は カゴに入る果物の数(8コ)の 何倍ですか?
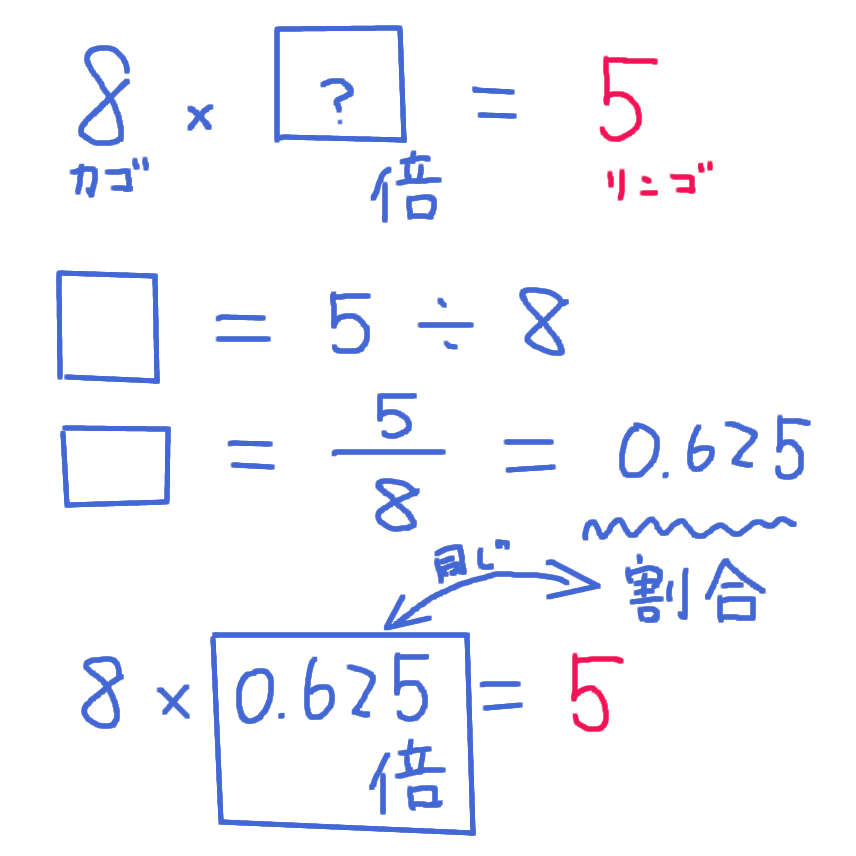
数だけを抜き取ると「5は 8の何倍ですか?」
5は 8の5/8倍 です。
5/8倍は 小数で表すと 0.625倍です。
この「0.625倍」の「0.625」という数字が「割合」になります。「62.5%」「6割2分3厘」などと呼ばれます。
「リンゴの数(5コ)は カゴに入る数(8コ)の何倍?」と考えれば、カゴに入る数(8コ)に対する リンゴの数(5コ)の「割合」を求めることができます。
カゴに入る数に対する リンゴの数の割合は「0.625」になります。
割合は分数で考える
果物が8コ入るカゴがあります。
3コのスイカがあります。

スイカの数(3コ)は カゴに入る果物の数(8コ)の 何倍ですか?

数だけを抜き取ると「3は 8の何倍ですか?」
3は 8の3/8倍 です。
3/8倍は 小数で表すと 0.375倍です。
先ほどと同様に「0.375倍」の「0.375」という数字が「割合」です。
「スイカの数(3コ)は カゴに入る数(8コ)の何倍?」と考えれば、カゴに入る数(8コ)に対する スイカの数(3コ)の「割合」を求めることができます。
分数から割合を想像する
割合は 小学校5年生の後半で学習します。割合を学習するまでに 分数を繰り返し学習しているので、「カゴの中に入るスイカの絵」を見たときに「3/8」を 容易に想像(連想)できる能力が身についているはずです。

8コ入るカゴの中に 3コのスイカが入っています。これはまさに「3/8」という状況です。
カゴに入る数(8コ)に対する スイカの数(3コ)の「割合」は、「3/8」であって 小数で表すと「3÷8=0.375」となります。

分数は計算をすすめる前の割り算 ⇒ 分数は割り算
もとにする量と 1
割合の話をもう少し進めます。

果物が8コ入るカゴがあります。
5コのリンゴがあります。
3コのスイカがあります。
果物が8コ入るカゴに 5コのリンゴと 8コのスイカを入れると カゴは満載状態です。

カゴに入る果物の数(8コ)に対するリンゴの数(5コ)の割合は「5/8 小数だと0.625」です。
カゴに入る果物の数(8コ)に対するスイカの数(3コ)の割合は「3/8 小数だと0.375」です。
5/8 + 3/8 = 8/8 = 1
なのでカゴが満載(8コ)の状態の割合は「1」になります。
「もとにする数を1とすると~」という あの不思議な文章は、カゴが満載の状態を表しています。
例えば
果物が8コ入るカゴと 8コのリンゴがありました(スイカは0コです)
カゴに入る果物の数(8コ)に対するリンゴの数(8コ)の割合は
8/8 = 8÷8 = 1
なので「1」になります。
「何倍?」で考えると
リンゴの数(8コ)は カゴに入る果物の数(8コ)の 何倍ですか?
8は 8の1倍なので「割合」で考えても「何倍?」で考えても 同じ「1」が現れます。

大切なことは
カゴに入る果物の数(8コ)に対する「割合」だということです。

スイカが3コ あってもなくても!カゴに入る果物の数(8コ)に対するリンゴの数(5コ)の割合は「5/8 小数だと0.625」になります。
全体の量 もとにする量
「割合」の単元以前は、リンゴの数(5コ)と スイカの数(3コ)を 足した数(8コ)は 積極的に着目されない数でした。

リンゴが5コありました。スイカが3コありました。
スイカ(3コ)からみると リンゴ(5コ)は どんな大きさですか?

リンゴ(5)は スイカ(3)の「5/3倍」です。
では
リンゴ(5コ)からみると スイカ(3コ)は どんな大きさですか?

スイカ(3)は リンゴ(5)の「3/5倍 小数だと0.6倍」です。
このように
5 = 3 × 5/3
3 = 5 × 3/5
この2つの式にしか 積極的な着目はありませんでした。
だけど「割合」の単元以降は リンゴの数(5)と スイカの数(3)を 合計した数(5+3=8)にも 着目が必要になります。

「リンゴに対する割合」と「スイカに対する割合」に加えて「リンゴとスイカを足し合わせた数に対する割合」にも 視野が拡張されています。

ちょっと長くなってしまいましたが、公式に頼らない割合の問題の考え方を うだうだと書きました。
どっちを割るのか分からない問題 ⇒ どっちを割るのか 分からない問題