分数は 計算をすすめる前の割り算です。
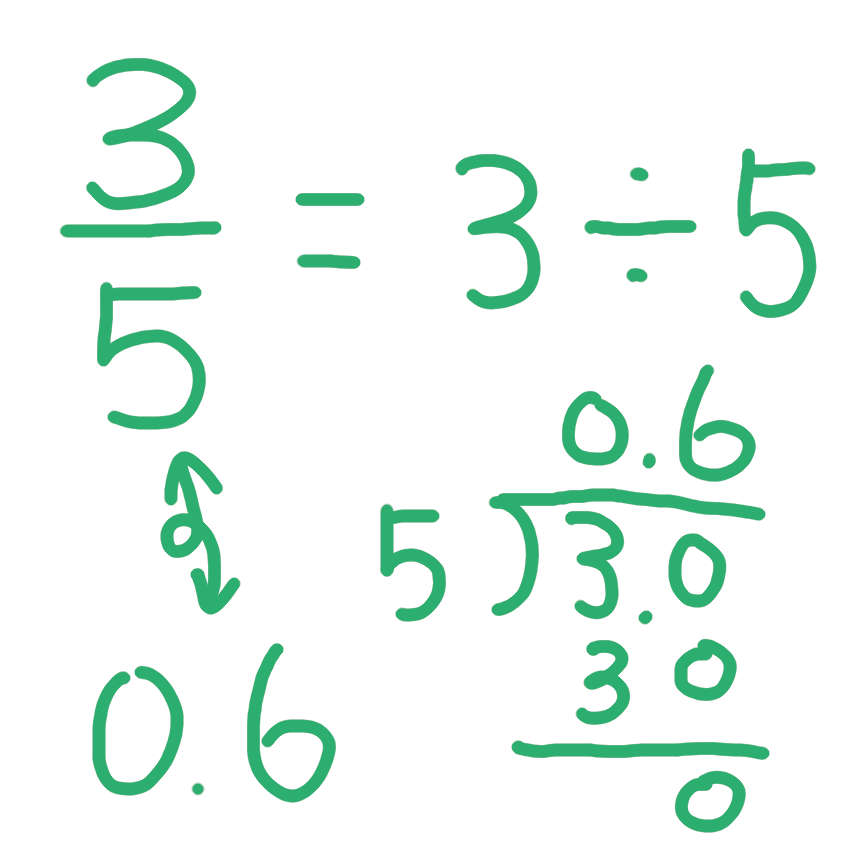
分数 苦手 小学校4年生 5年生 小学生 算数
分数は 計算を始める前の割り算です。3/5(5分の3)は 3÷5に相当(同じ意味 同義)します。
もっと安直な表現をすると、分数は「割り算」です。
小学校5年生で、小数点以下まで割り進む 割り算を勉強します。例えば、上に挙げた「3÷5=0.6」が、計算できるようになります。
ここで ようやく! 分かりにくかった 分数の正体(概念)に 触れる手段が、整います。
分数も 数の表し方のひとつ
小学校2年生で、割合的な意味に おもきを置いて 分数の勉強が始まります。(教科書の誘導からは、割合や等分というニュアンス(意図)が 強いような印象を 受けます。)

ですが、分数だって、整数や小数と同じように 数直線上に示すことができる 数の表し方のひとつです。
分数も 「数の表し方」の ひとつです。
ここが、「分数って何?」から 開放されるための 第1歩です。
具体的に「1÷5=0.2」「3÷5=0.6」など、分数を割り算になおして 計算してみましょう。
分数は 上 ÷ 下
分数を割り算になおすとき「上 ÷ 下」と覚えると、字の形から 分子と分母の関係を 想像しやすくなります。

「上」という文字の長い横棒
「下」という文字の長い横棒
割り算の記号が 「上 ÷ 下」という分数の形に 見えてきます。

分数は 上÷下の 割り算です。
分数を 割り算することで、小数に 変換することができます。
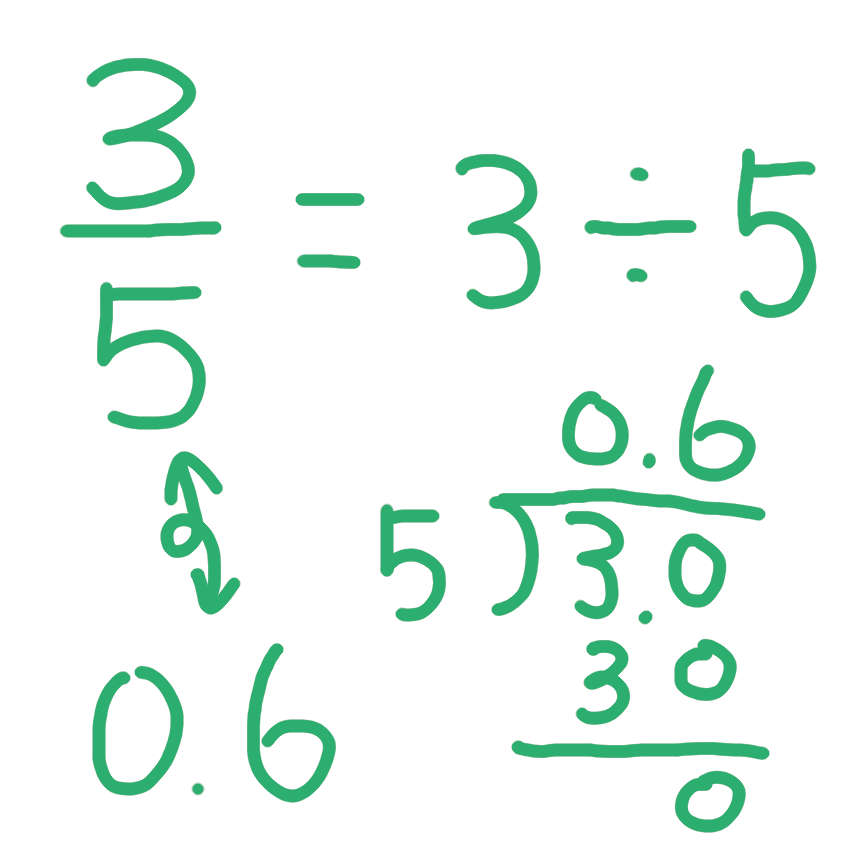
3/5(5分の3)と 3÷5と 0.6は、すべて同じ値(量)を表します。
分数と 割り算と 小数
3/5(5分の3)のように、割り切れる場合もあれば
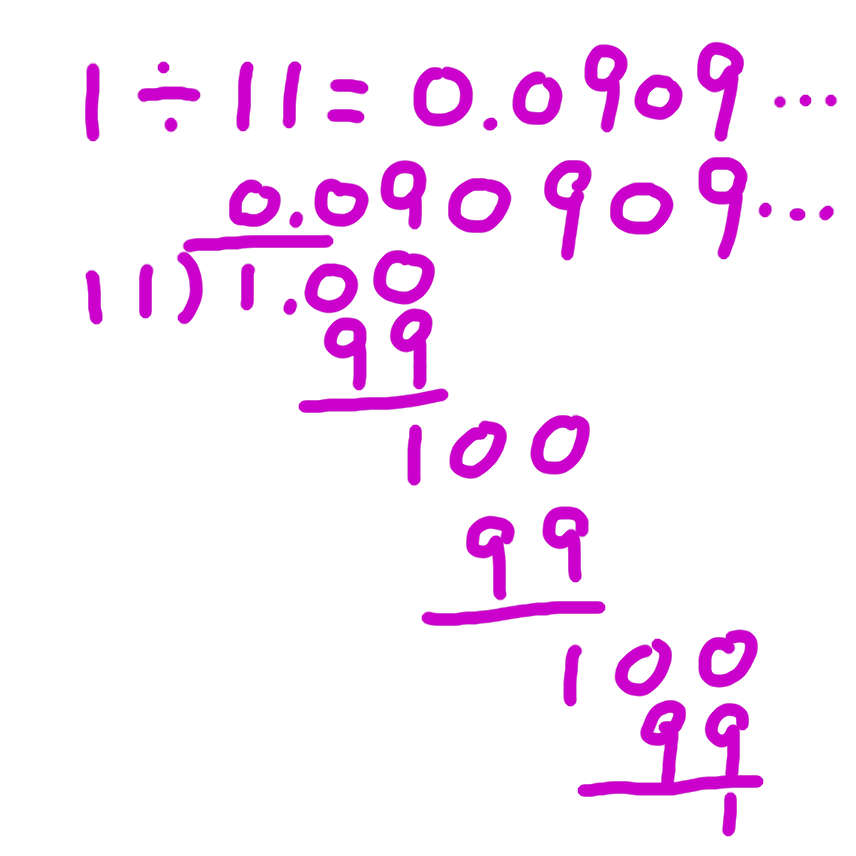
1/11(11分の1)のように、同じ数字が繰り返しあらわれて、いつまでも続く場合もあります。
0.0909090909...
このように伝えるよりも
1/11(11分の1)と伝えたほうが 分かりやすい場合があります。こういうときに、分数を使います。分数は、仕組みが分かると とても便利に使える「数の表し方のひとつ」です。
そもそも論 ですが、0.09090909...という状況は、1/11を割り算した結果に出現する小数とも 考えられます。2つの数字(1と11)の関係を示したいとき、割り算を省略して 分数の形で もとの2つの数字(1と11)をそのまま使って、数を表していることになります。
分数とは、2つの数字の関係を使って表した「数の表し方のひとつ」とも表現できます。
小数と分数の使い分け
小数には、精度(粒度)をあげていくような、拡大していくようなイメージがあります。

例えば 量り(はかり)で 重さを量るとき、メモリとメモリの間まで 細かく読みます。こういう状況のときは、小数を使って表す方法が 一般的です。
分数と割合
一方で 分数は、割合を考える場面で 使われることが、多いと思います。
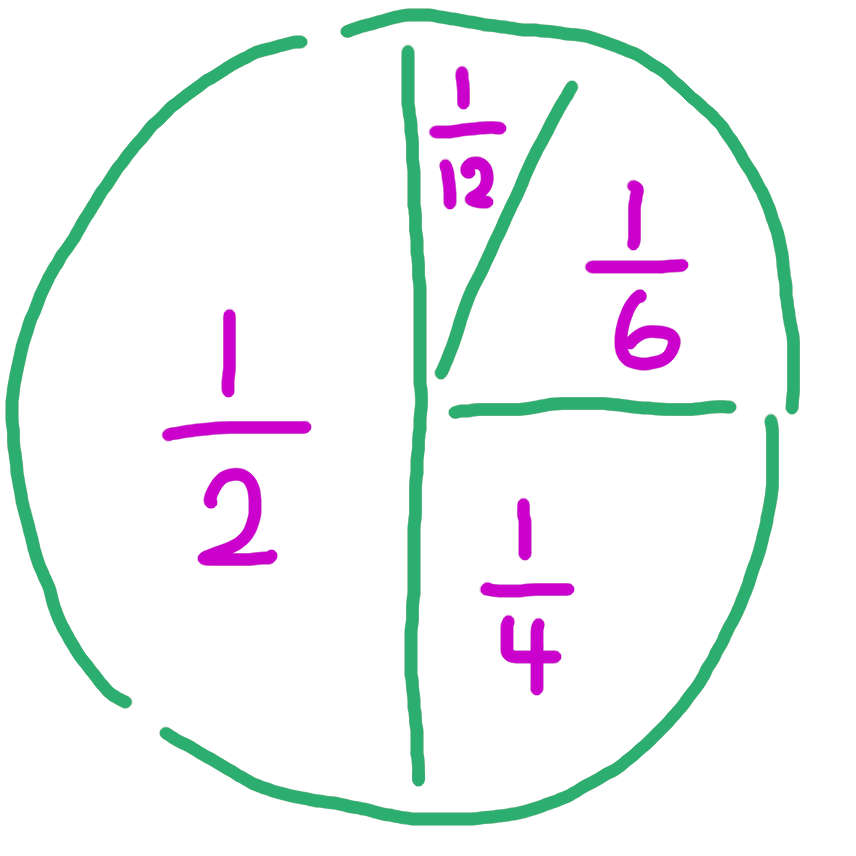
2つの量の関係、どちらか片方を基準としたときに もう片方は どれくらいの大きさなのか。
繰り返しになってしまいますが、2つの量(数字)の関係を 2つの数字を直接 そのままに 使って表した数が 分数です。
分数は 割り算
分数は 割り算をして 小数に変換してしまえば、大きさを表す 数の表し方のひとつ だということが、感覚的に分かりやすくなります。
ちょっとだけ強引にまとめると、「数の表し方のひとつ」という側面と、「割合を表すときの手段に使われがち」という側面を、分数は あわせ持っています。
ここが ごっちゃになってしまい、「よく分からん・・・」状況になってしまうことが多いと思われます。
いっぬ。

分数の苦手を克服してほしい ⇒ 分数の苦手を克服してほしい