3の4倍は 12です。
3 × 4 = 12
これが分かれば割合の問題を解くことができます。割合とは「何倍?」の言いかえです。
「ある牧場の 今年のブタの数は 120人です。来年のブタの数は 今年の250%(2.5倍)になる予定です。来年のブタの数は 何人になる予定でしょうか?」
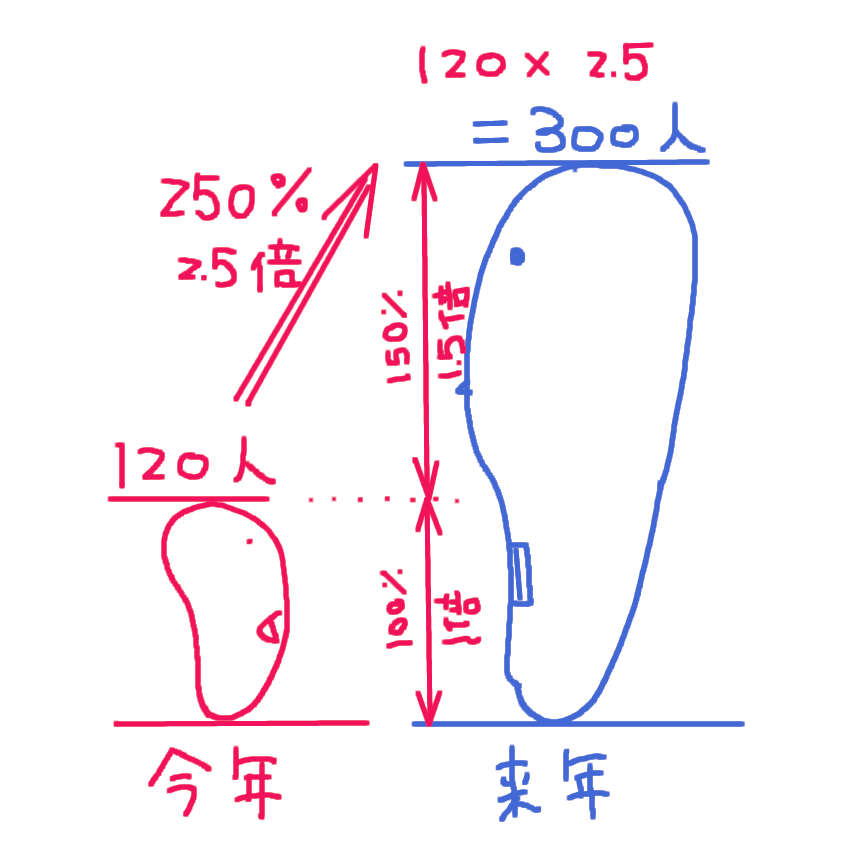
来年のブタの数は 今年のブタの数(120人)の2.5倍(250%)です。
120 × 2.5 = 300
来年のブタの数は 300人です。
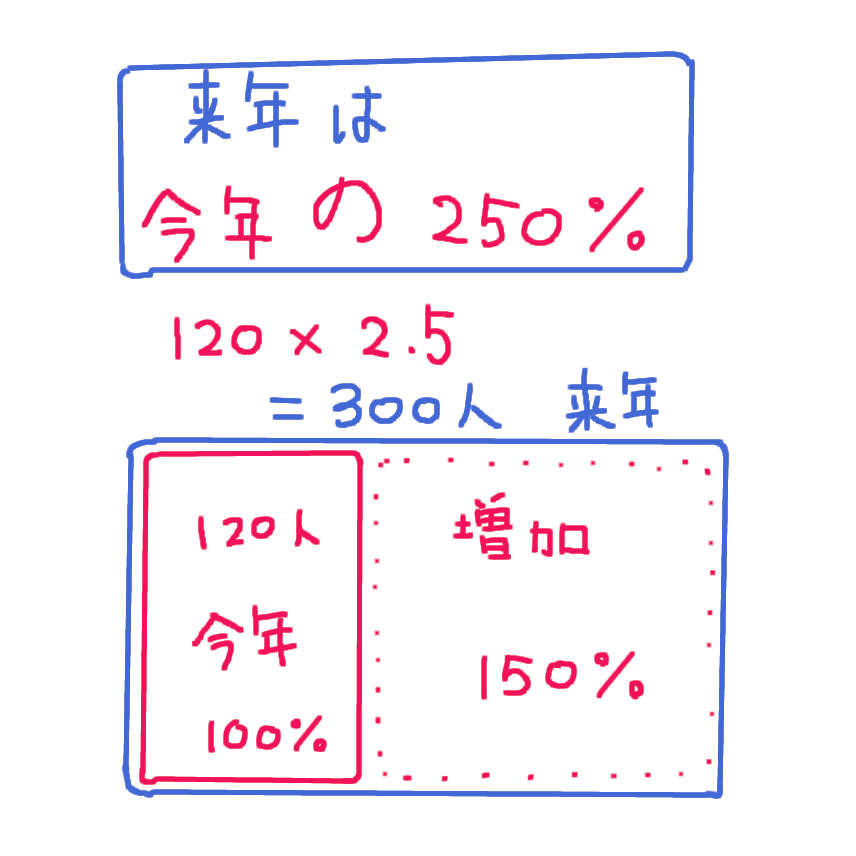
基準量 比較量などの(呪文のような)言葉と公式を使わなくても 割合の問題が解けるようになります。
公式を使わない 割合の問題の考え方
3の4倍は 12です。
3 × 4 = 12
このかけ算が想像できる人ならば 公式を使わずに 割合の問題を解くことができます。割合とは「何倍?」の言いかえです。
「ある牧場の 今年のブタの数は 120人です。昨年のブタの数は 今年の85%(0.85倍)でした。昨年のブタの数は 何人でしたか?」
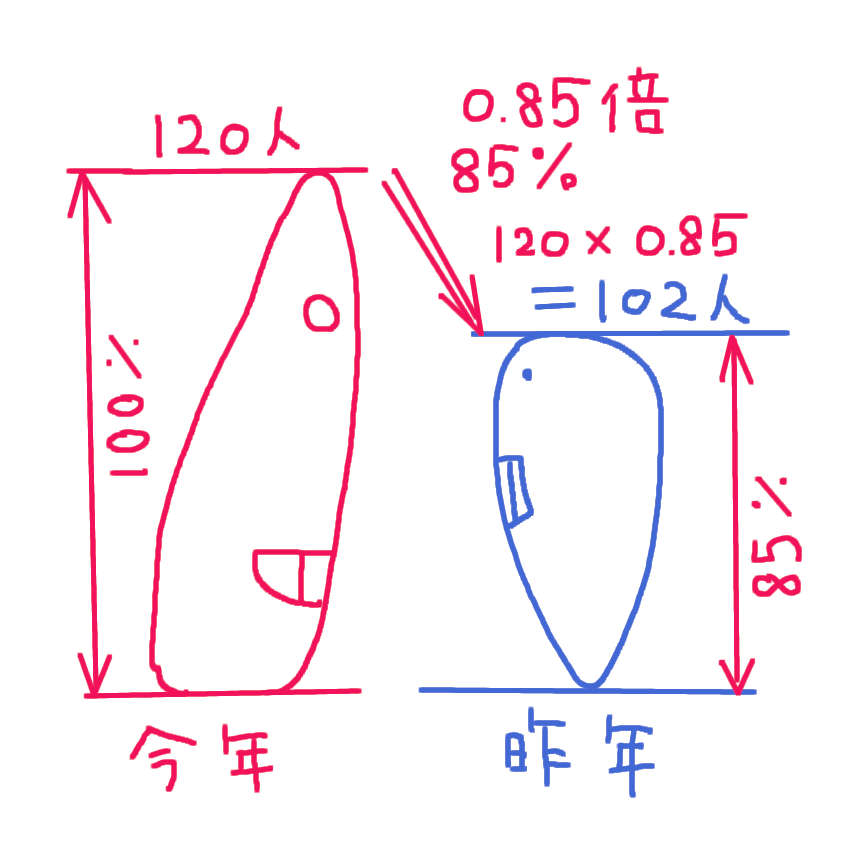
昨年のブタの数は 今年のブタの数(120人)の0.85倍(85%)です。
120 × 0.85 = 102
昨年のブタの数は 102人です。
どっちから どっちを見るのか。
今年から ⇒ 昨年を ながめるイメージです。今年の 0.85倍が ⇒ 昨年です。

今年を100%と考えているので 昨年は(今年よりも 15%少ない)85%と表すことができます。
▲↑▲ こんなイメージです。
公式を使わない 割引と割合の問題
「定価3000円のカステラが 20%引きの値段で売られています。このカステラは いくらで買えるでしょうか?」
大人になると 割合の問題は 自然に解けるようになります。状況が イメージできるようになるからです。
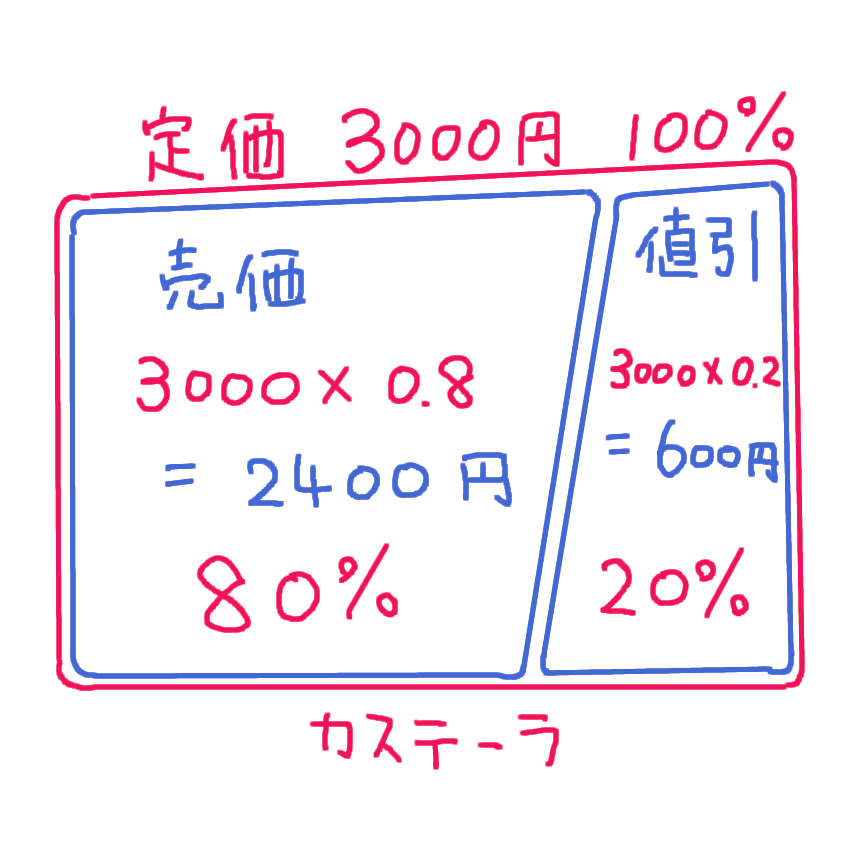
定価が100%で 20%引きで販売されているので、売価は 定価(3000円)の80%(0.8倍)になります。
3000 × 0.8 = 2400
20%引きのカステラの売価は 2400円です。
大人は 上の図が 自然とイメージできます。基準量 比較量などの 謎の呪文(公式)をとなえる前に 上の図のようなイメージを共有すると 割合の問題が解けるようになります。
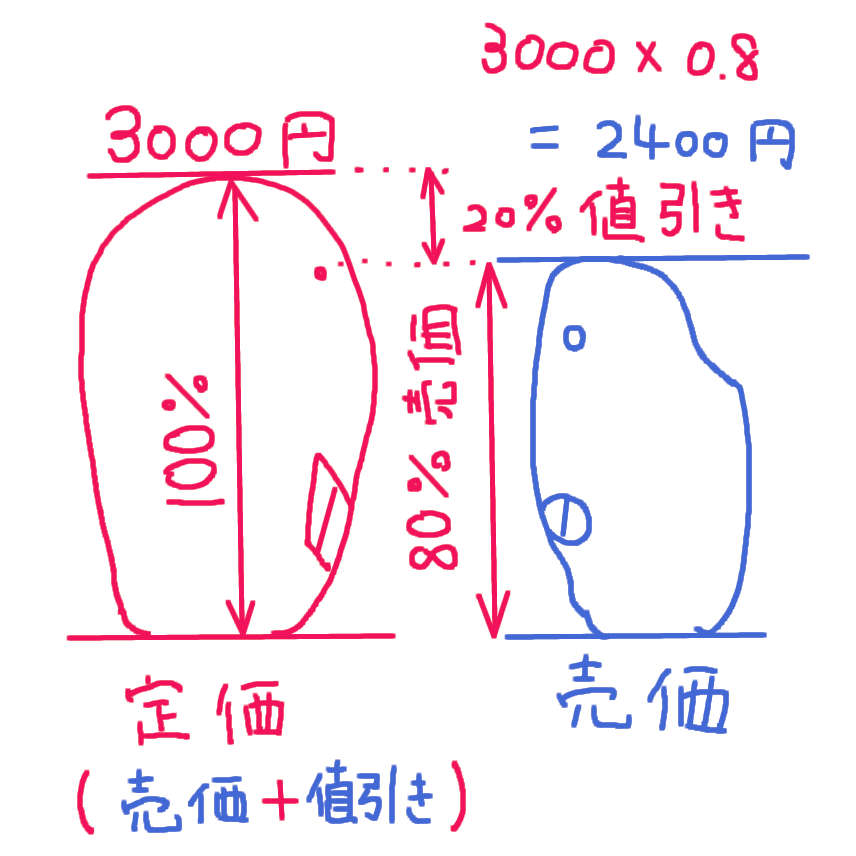
定価(100%)から ⇒ 売価(80%)をながめる イメージです。定価(3000円)の ほにゃらら倍(0.8倍)が 売価(2400円)になります。
公式を使わないで 割合(百分率)を求める
3 × ロ = 12
ロ = 12 ÷ 3 = 4
ロ = 4
この仕組みが想像できれば、割合の問題を解くことができます。
「ある牧場に 75人のブタがいます。大人のブタは45人 子供のブタは30人 です。牧場のブタ全員(75人)に対する 大人のブタの割合を百分率で求めましょう。」
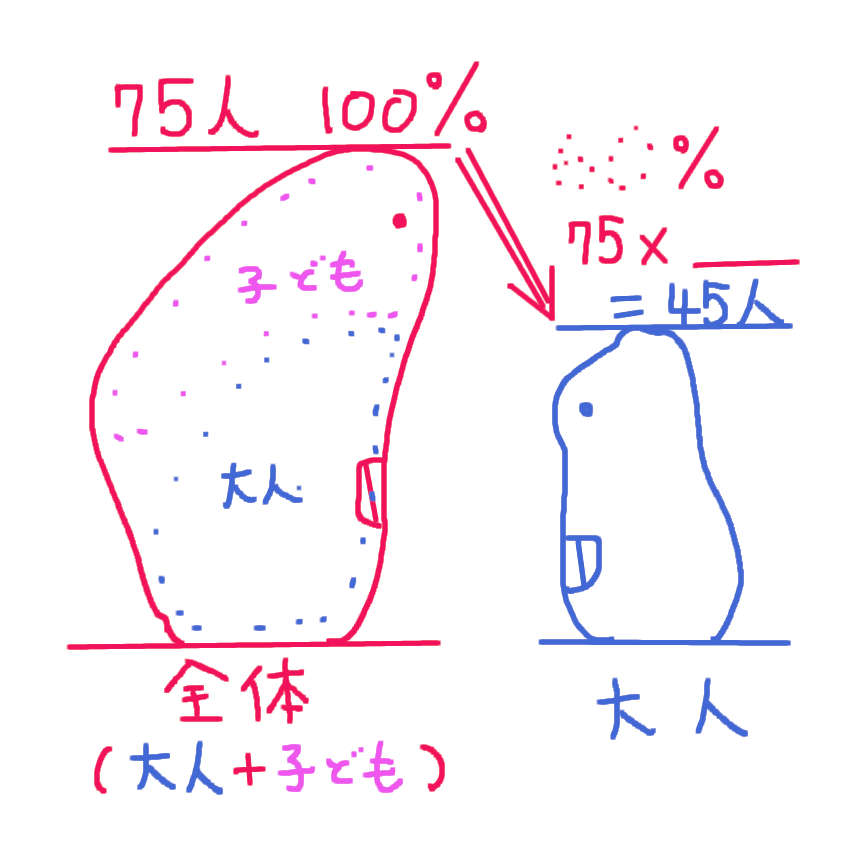
ブタ全員(75人)に対する 大人のブタ(45人)の割合を求めるためには 上のようなイメージを想像します。
ブタ全員(75人)の ほにゃらら倍が 大人のブタ(45人)になっています。
75 × ロ = 45
ロ = 45 ÷ 75
ロ = 0.6
0.6倍は 60%なので、大人のブタの割合は 60%になります。
どっち(ブタ全員)から ⇒ どっち(大人のブタ)をながめるのか 日本語と照らし合わして イメージします。

「ブタ全体に対して 大人のブタの割合は いくつなのか? 」という日本語と「大人のブタは ブタ全体の何倍なのか?」という日本語は、使われている単語は違えど 同じ意味になります。

上のイメージのような状況を 共有したいとき、「大人のブタは ブタ全体の75%」という方法もあれば「ブタ全体に対する 大人のブタの割合は75%」という方法もあります。
3 × 4 = 12
3の4倍は 12です。
割合の問題は、このような ちょっとしたかけ算と (実は)日本語の問題です。

大人になると 日本語が(少なくとも小学校5年生にくらべると)上手に使いこなせるようになるので、割合の問題が 自然と!解けるようになります。
というわけで、(公式を使わずに)日本語を上手に使って 割合の問題を解くお話でした。
ぶひぶひぶひ

割合の問題は「何倍?」を考えると解ける ⇒ 割合の問題は「何倍?」を考えると 解きやすい