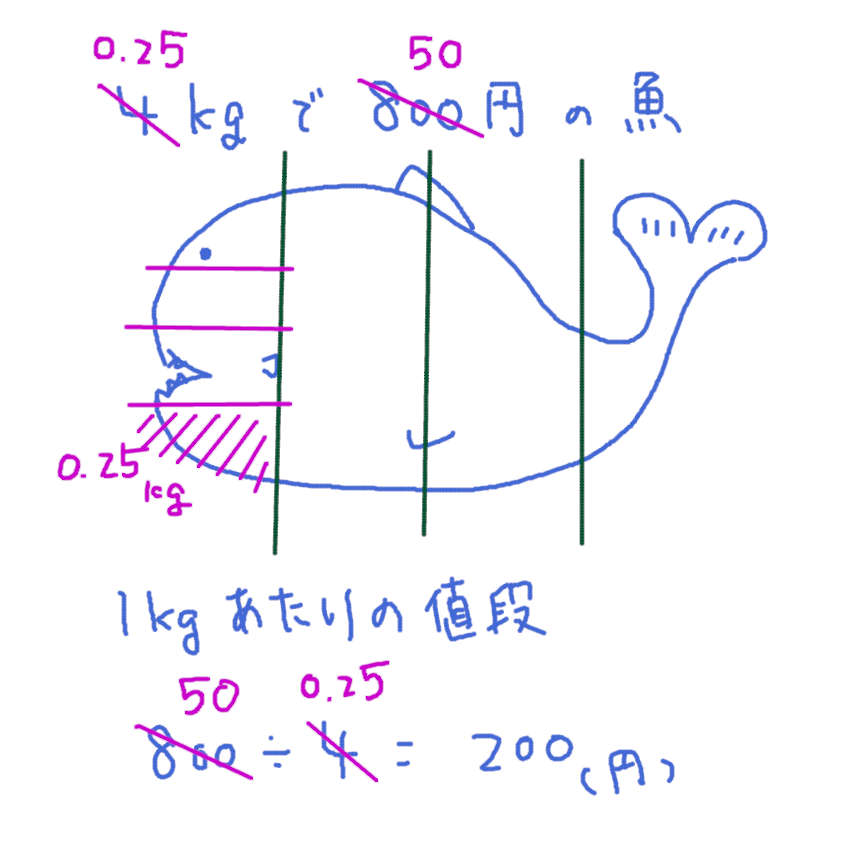
「4kgで 800円の お魚が売っています。1kgあたりの値段は いくらですか?」

とにかく 絵を描く作戦で進みます。
「値段 ÷ 重さ」です。なので 1kgあたりの値段は200円です。
次は
「3kgで20円のお魚が売っています。1円あたりの重さは何kgですか?」

絵心が欲しいです。1円あたりの重さは0.15kgです。
「重さ ÷ 値段」なので、割る数と割られる数が さっきの問題と逆転します。どっちを割る数にして どっちを割られる数にするのか、絵を描きながら考えます。
割る数と割られる数が入れ替わることで 何を計算したことになっているのか、絵を描いて状況を整理します。

整数だったら分かるのに、小数になると 迷子になってしまいます。
まずは簡単な整数に置き換えて 絵を描いて式を立てて、よさそうならば 小数に数字を戻して考えると 納得感が出てきます。

割合の問題で困っている場合は このページがいいかもしれません ⇒ 割合の問題は「何倍?」を考えると 解きやすい

割られる数よりも 答えが大きくなる割り算の不思議 ⇒ 割り算 割られる数よりも 答えが大きくなる理由
割られる数ってどっち?
「重さが5kgのネコと 重さが20kgのブタがいます。ネコの重さは、ブタの重さの 何倍ですか?」

ネコの目線で ⇒ ブタを見るのか。
ブタの目線で ⇒ ネコを見るのか。
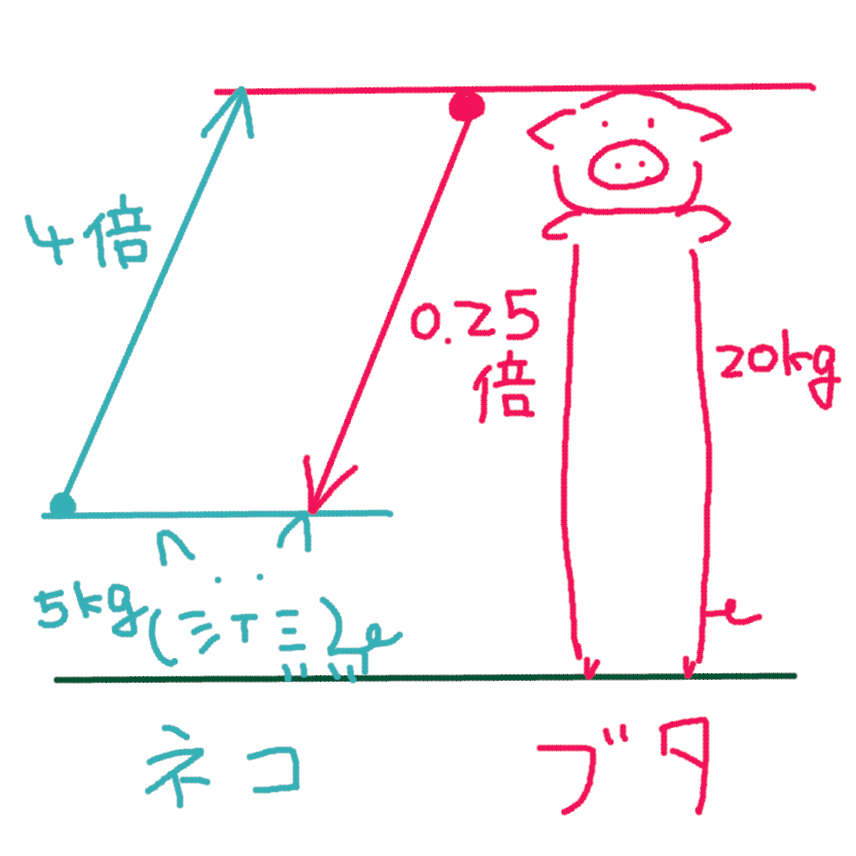
「何倍ですか?」
このような問題のとき、登場人物は 2人以上 出現します。今回はネコとブタです。
2人(2匹?)の関係を 算数の式を使って表したいとき、2つの方法があります。

ネコの目線でブタを表す方法。
ネコ×4=ブタ
または

ブタの目線でネコを表す方法。
ブタ×0.25=ネコ
このように 2人の関係は 2通りの方法で 表すことができます。
ネコ×4=ブタ
ブタ×0.25=ネコ
これ、とても重要です。
「重さが5kgのネコと 重さが20kgのブタがいます。ネコの重さは、ブタの重さの 何倍ですか?」
この質問の場合は、「ブタの目線」で「ネコ」の重さを表したい。


ブタ×○=ネコ
○=ネコ÷ブタ
かけ算の式を想像してから問題を解くと、どっちをどっちで割るのか、間違いにくくなります。

似たような文章題を解くお話 ⇒ 苦手な文章題を解くヒント
日本語の中の「の」と「は」の お話です。

公式を使わない割合の問題の考え方 ⇒ 公式を使わない割合の解き方を考える
どっちを割るのか 分からない問題
(ここから先は ちょっと 大人向けかも?)
「重さが5kgのネコと 重さが20kgのブタがいます。ネコの重さは、ブタの重さの 何倍ですか?」
小学校5年生 少数の割り算を習うと、こんな問題が登場します。正確には、小学校4年生で 少数の割り算を学習すると、このような類(たぐい)の問題を出題できるような概念が 出そろうことになります。
少なくはないお客様(お子様)は、20÷5=4 答え 4倍 と回答し、ぶッぶーと なります。
最初はみんな そんな感じです。
どっちを どっちで割るのか分からない問題。割る数と割られる数が分からない 逆になってしまう問題。割られる数よりも 割る数が大きい問題。教えるときのヒントになればうれしいです。
どっちを どっちで割る 割り算なのか
「重さが5kgのネコと 重さが20kgのブタがいます。ネコの重さは、ブタの重さの 何倍ですか?」

5÷20=0.25 答え 0.25倍
これが正答になります(少数でも分数でも どちらでもよいかと)
では、どうやって伝えると 分かりやすくなるのか。
上に載せた図(絵?)が ひとつの大きなヒントになります。5と20という ふたつの数が どのような関係なのかを表したいときに、4倍という表し方と 0.25倍という表し方の 2通りが存在します。
(もっと正確には、20-5=15 5-20=-15 のように加減を使って2つの数の関係を表すこともできるので、2通り以上の表し方が存在しています)
4倍と0.25倍は、何が違うのか。というと「どっちの数字から どっちの数字を見ているのか」が違います。
5を基準にして 20をみると 5×4=20 となり、5の4倍が20になります。
20を基準にして 5をみると 20×0.25=5 となり、20の0.25倍が5になります。
ここで大切なのは、2つの数の関係を考えるときに「いきなり割り算の式を」導き出して「何倍か?」を求めようとすることは、慣れるまでは 難しい思考だと 認識することです(人それぞれ 得意不得意は ありますが)
引き算よりも足し算、割り算よりもかけ算を 先に習うような学習体系も手伝って、多くの場合は かけ算という概念が 土台として使いやすいように感じます。
何倍ですか? 割り算?
「何倍ですか?」と 問われたとき。
視野を広げると、それはすなわち、「そこに提示された ふたつの数が どのような関係になっているのか、認識できますか?」
と、このように読みかえることができます。
ふたつの数が どのような関係なのかを 表現したいときに、「何倍」という手段(考え方)と かけ算という 数学言語的な表し方(こちらも手段)が 存在するのです。
どうでしょうか。話がややこしく 感じられるでしょうか。
「どっちを どっちで割るのか 分かるようになる」「割る数と割られる数を 間違えないで選ぶ」ということは、上でお伝えしたような(抽象的な?)概念を理解するということになります(と 僕は考えています)
このようなことを伝えるのは、とても難しい作業だと思います。学校の先生や お父さんお母さんの苦労が、身に染みて伝わってきます。
「何倍ですか?」と問題文に書いてある場合は「割り算をしましょう」といった 安直で単純な説明が、できなくなってくるからです。
割られる数よりも 割る数が 大きい問題
(僕の言葉の選び方が 下手で)日本語が分かりにくい部分もあるかと 思います。ゆっくり お読みくださると うれしいです。

リボンの長さや 木の高さ、砂糖と塩の重さなどが例となって、出題されることが多いです。絵に描くことで、話が具体的になるので、状況を理解するきっかけが 見つかりやすくなります。
「高さが4mの木と 高さが8mの木が 立っています。4mの木は 8mの木の 何倍の高さですか?」
このように、どちらか片方を基準としたときの関係だけを(回答として)求められる問題が、多く出題されます。
ですので、「8mの木を基準にしたときに(もとにすると)、4mの木は何倍の大きさなのか」を確認したあとで、「4mの木を基準にしたときに(もとにすると)、8mの木は何倍の大きさなのか」も あわせて確認します。
そうすることで、ふたつの数の関係を表すときの 基準の違いによる 2通り以上の表し方の存在が、分かりやすく説明できます。
はて、ちょっと長くなってきました。
割り算の文章問題が 難しい
そもそも。割り算なのか かけ算なのか。どっちを選べばいいのか 判断が難しい お客様(お子様)も、少なくはありません。
かけ算 割り算を問わず 文章題が苦手と、相談されることも 多くあります。
小学校4年生までは、かけ算の範囲の場合は かけ算を、割り算の範囲の場合は 割り算を していれば(演算すれば)、その単元の文章題で 得点することができました。
ですが、小学校5年生よりも学年があがると、加減乗除 四則演算の中の どの演算が必要なのかを判断し 選択する能力が、明確に求められるようになります。
こうなると、文章問題で説明されている出来事の状態(全体図)を、理解する必要が でてきます。
言い方を変えると、日本語(言語)を読み 状況を理解する力が、必要になってきます。

教わる側(お子様)の 知っている言葉の数(語彙 vocabulary)は、伝える側(大人)に比べて 圧倒的に少ない状況となります。
ですので、伝える側(大人)は、「もとにする」だとか「基準にする」などの言葉の意味(概念)を きちんと かみくだいて 分かりやすく説明する必要があります。
飲み込むまでに 時間がかかったり、1度伝えたはずのことが 分からなくなってしまったり、当然に頻繁に 起こり得ます。
ゆっくりあせらずじっくりです。
具体的な教え方 伝え方
ページの最初に載せたような絵を いろいろなパターンで描き続け、ふたつの数の関係という 概念と状況を、適切な日本語とともに伝えます。
例えば 楽しいときや うれしいときに、その感情の変化を呼び起こした出来事を 周りの大人も一緒になって体験し 日本語で表現することで、言葉の意味と概念を理解していく状況に 近い状態でしょうか。
中学生になってからも、割合や%の問題、食塩水の濃さや 消費税の問題として、ふたつ以上の数の関係を問われる問題が たくさん出題されます。
小学生の段階で この分野の概念をしっかりと身につけることで、中学校に入ってからの数学が とても楽ちんなものになります。
というわけで。
どっちを割るのか 分からない問題について、長々と語ってみました。少しでもお役に立てれば幸いです。
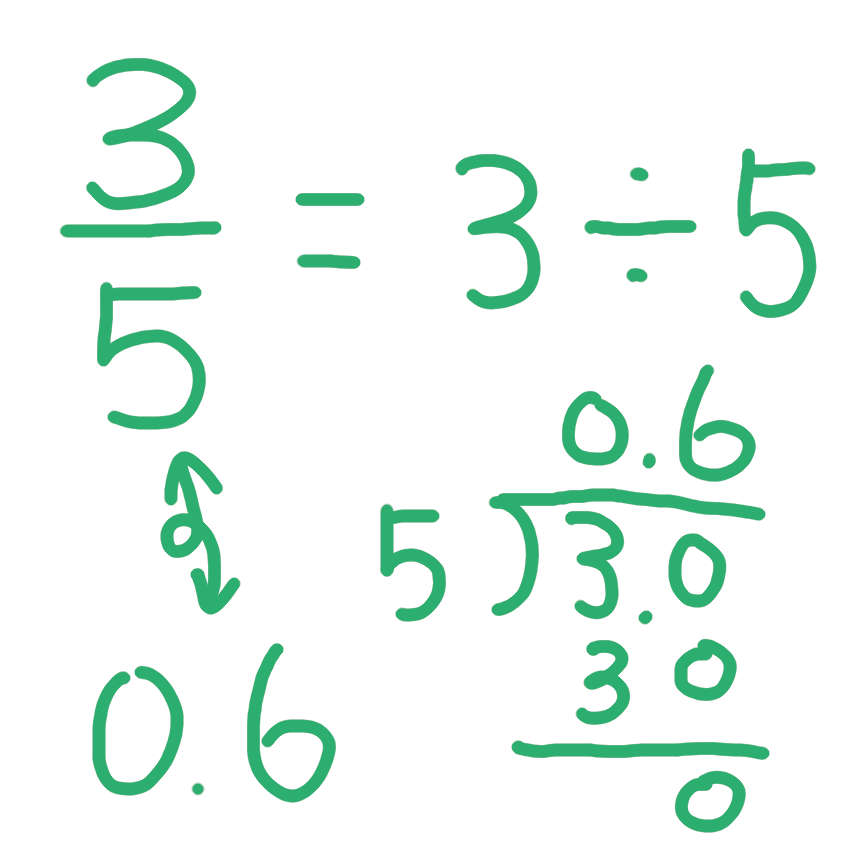
分数は 計算をすすめる前の割り算 ⇒ 分数は割り算

学校の先生と 塾の先生の教え方は 違うかも ⇒ 学校の先生と 教え方が違うときがあります