中学校 数学 で習う 正負の数の計算方法(足し算 引き算 かけ算 割り算)について、もうちょっと分かりやすい(と思われる)解説ページを書きました。

正負の数の計算は まずは かけ算から覚えてほしい ⇒ 正負の計算は かけ算から覚えると簡単 中学生 数学
▲↑▲ こっちの記事を先に読んでほしいです。

中学生になると 負の数(マイナスの数)にまで 数学の学習範囲が拡張されます。まずは5つのルールを覚えます。

小学校までは「4」はただの「4」でしたが、中学校からは「+4」なのか「-4」なのかを区別します。
なぜ「(+4)」このようにカッコ()をつけるのか?
なぜならば「(+4)」のように正の数を表す「+」の符号と 「4+3」のように足し算を意味する「+」の計算記号を 区別するためにカッコを使います。

▲↑▲ 数式の先頭の「+」は省略されます。
また、カッコの前と カッコの中で同じ符号が連続したとき ⇒「+(+3)」は、「+3」のように「+」に置き換わることでカッコが省略されます。
カッコの外し方を説明します。
正負の数の 足し算と引き算 カッコの外し方 覚えやすい考え方
正負の数の足し算と引き算における カッコの省略方法(外し方)を書きます。ルールは3つです。

▲↑▲ カッコの前と カッコの中で 異なる符号が並んだとき ⇒「-(+3)」もしくは「+(-3)」は、「-3」のように「-」に置き換わることでカッコが省略されます。
もう1度書きます。
カッコの前と カッコの中で 異なる符号が並んだとき ⇒「+(-7)」は、「-7」のように「-」に置き換わります。
ようするに
「+と-の組み合わせ」は「-」になります。

▲↑▲ カッコの前と カッコの中で 同じ符号が連続したとき ⇒「-(-3)」もしくは「+(+3)」は、「+3」のように「+」に置き換わることでカッコが省略されます。
もう1度書きます。
カッコの前と カッコの中で 同じ符号が連続したとき ⇒「-(-7)」は、「+7」のように「+」に置き換わります。
ようするに
「+と+の組み合わせ」と「-と-の組み合わせ」は「+」になります。
ここまでをまとめます。
-
数式先頭の「+」は省略
-
同じ符号の組み合わせ「+ +」「- -」は ⇒「+」
-
異なる符号の組み合わせ「+ -」「- +」は ⇒「-」
ルールは↑の3つだけです。もう1度 絵を見ます。

▲↑▲ 数式先頭の「+」は省略されます。
カッコの前と カッコの中で 同じ符号が連続したとき ⇒「-(-3)」もしくは「+(+3)」は、「+3」のように「+」符号になります。

▲↑▲ 数式先頭の「+」は省略されます。
カッコの前と カッコの中で 異なる符号が並んだとき ⇒「-(+3)」もしくは「+(-3)」は、「-3」のように「-」符号になります。
-
数式先頭の「+」は省略
-
同じ符号の組み合わせ「+ +」「- -」は ⇒「+」
-
異なる符号の組み合わせ「+ -」「- +」は ⇒「-」
ルールは↑の3つだけです。これだけ覚えれば ひとまずカッコは外せます。
マイナスの数の加法減法 加算減算 足し算引き算 覚え方
カッコを省略したあとの計算のルールは2つです。
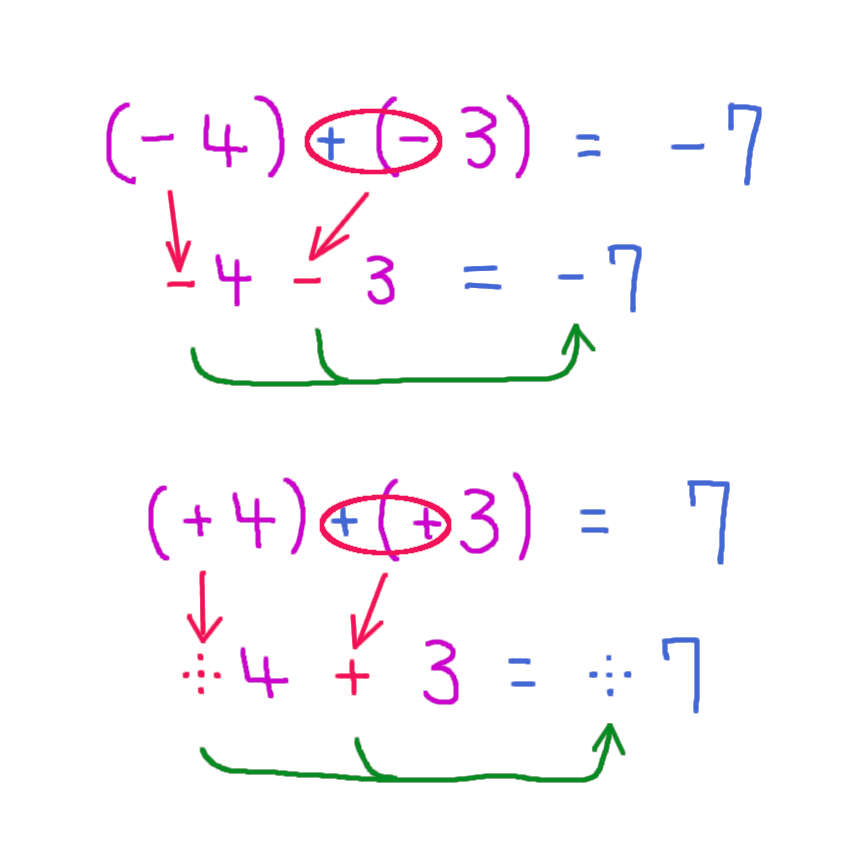
▲↑▲「-4-3」のように同じ符号「-」の項が並ぶとき ⇒「-4」と「-3」の絶対値の和(4+3=7)を(足し算で)求め 同じ符号「-」を与えて答えにします ⇒「-4-3=-7」。
「+4+3」のように同じ符号「+」の項が並ぶとき ⇒「+4」と「+3」の絶対値の和(4+3=7)を(足し算で)求め 同じ符号「+」を与えて答えにします ⇒「+4+3=+7」。
ようするに
同じ符号の項が並ぶとき ⇒ 絶対値の和を求め その和に同じ符号を与えて答えにします。

▲↑▲「-4+3」のように異なる符号「-と+」の項が並ぶとき ⇒「-4」と「+3」の絶対値の差(4-3=1)を(引き算で)求め 絶対値が大きい項「-4」の符号「-」を与えて答えにします ⇒「-4+3=-1」。
「-3+4」のように異なる符号「+と-」の項が並ぶとき ⇒「-3」と「+4」の絶対値の差(4-3=1)を(引き算で)求め 絶対値が大きい項「+4」の符号「+」を与えて答えにします ⇒「-4+3=-1」。
ようするに
異なる符号の項が並ぶとき ⇒ 絶対値の差を求め その差に絶対値が大きい項の符号を与えて答えにします。
ここまでをまとめます。
カッコを外したあとは
-
同じ符号 ⇒ 絶対値の足し算と 同じ符号
-
異なる符号 ⇒ 絶対値の引き算と 絶対値が大きい項の符号
ルールは↑の2つです。
もう1度 絵を見ます。
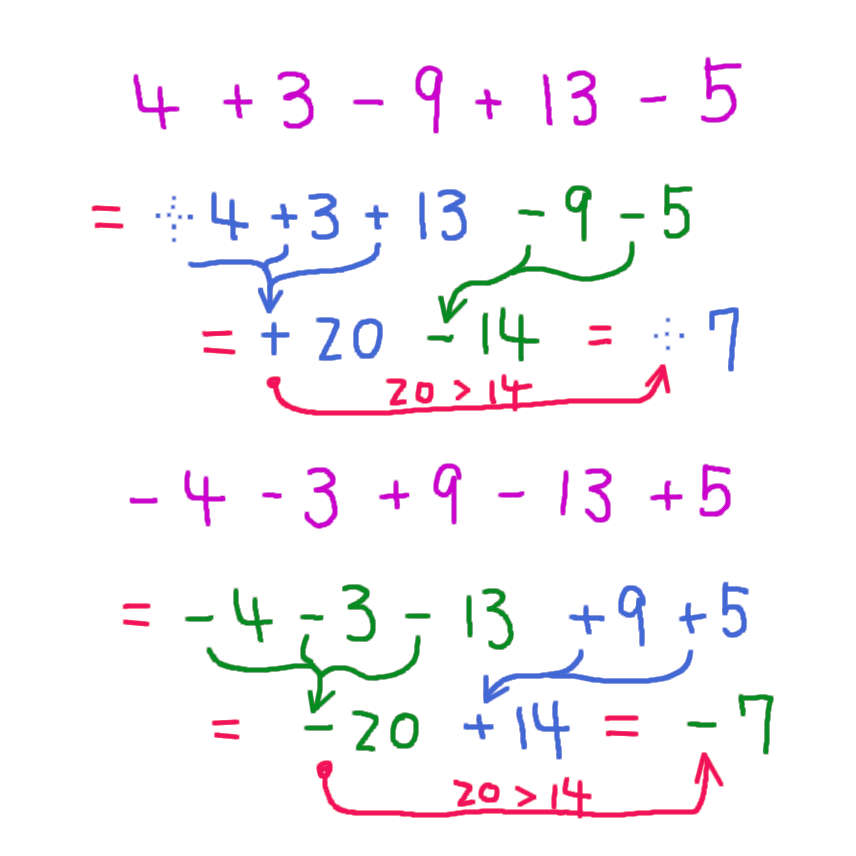
▲↑▲ 上段(4+3-9+13-5=+7)の解説
「+」の項(+4+3+13)と「-」の項(-9-5)に 並べ替えます。
同じ符号「+」の項が並んでいる「+4+3+13」は 絶対値の足し算を行い(4+3+13=20)同じ符号「+」を与えます ⇒「+20」
同じ符号「-」の項が並んでいる「-9-5」は 絶対値の足し算を行い(9+5=14)同じ符号「-」を与えます ⇒「-14」
異なる符号の項が並ぶ「+20-14」は 絶対値の引き算を行い(20-14=7)絶対値が大きい項「+20」の符号「+」を与えます ⇒「+7」
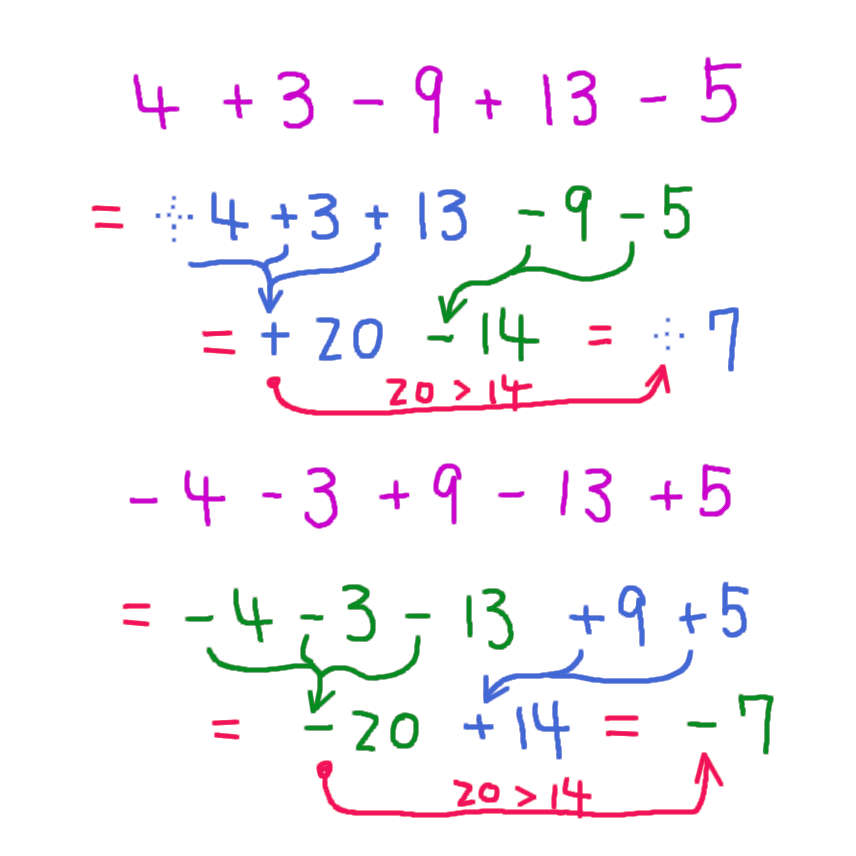
▲↑▲ 下段(-4-3+9-13+5=-7)の解説
「-」の項(-4-3-13)と「+」の項(+9+5)に 並べ替えます。
同じ符号「-」の項が並んでいる「-4-3-13」は 絶対値の足し算を行い(4+3+13=20)同じ符号「-」を与えます ⇒「-20」
同じ符号「+」の項が並んでいる「+9+5」は 絶対値の足し算を行い(9+5=14)同じ符号「+」を与えます ⇒「+14」
異なる符号の項が並ぶ「-20+14」は 絶対値の引き算を行い(20-14=7)絶対値が大きい項「-20」の符号「-」を与えます ⇒「-7」
もう1度書きます。
カッコを省略したあとは
-
同じ符号 ⇒ 絶対値の足し算と 同じ符号
-
異なる符号 ⇒ 絶対値の引き算と 絶対値が大きい項の符号
ルールは↑の2つです。
カッコを省略するためには
-
数式先頭の「+」は省略
-
同じ符号の組み合わせ「+ +」「- -」は ⇒「+」
-
異なる符号の組み合わせ「+ -」「- +」は ⇒「-」
ルールは↑の3つです。
この5つのルールを覚えれば、正負の数の足し算引き算が できるようになります。
負の数の 足し算と引き算 中学生 数学
小学校の算数と 中学校の数学では、数式の見え方(感じ方?)が 変化します。(気がつかないうちに変化しているはずです。)

小学校(算数)では「3+13-9」のように「ひとつの塊」として数式を把握します。中学校以上(数学)では「+3」「+13」「-9」というように項を意識しながら数式を読み書きします。
「+」と「-」の記号が 足し算と引き算の演算を意味する計算の記号から、各項の「正」と「負」 を表す記号(符号)に変化します。
「正」の数が何個ありますか?
「負」の数が何個ありますか?
という状況を数式が表すようなとらえ方になります。
(中学校以上の)数学では、(小学校的で直接的な)足し算と引き算の演算は 数式から姿を消します。(ちょっと強引な伝え方になってしまいますが。)
「+」
この記号は、直接的に足し算を意味しなくなります。
「-」
この記号も、直接的に引き算を意味しなくなります。
正の数 負の数 仕組み
まずは、5つのルールをガチガチに覚えてほしいです。
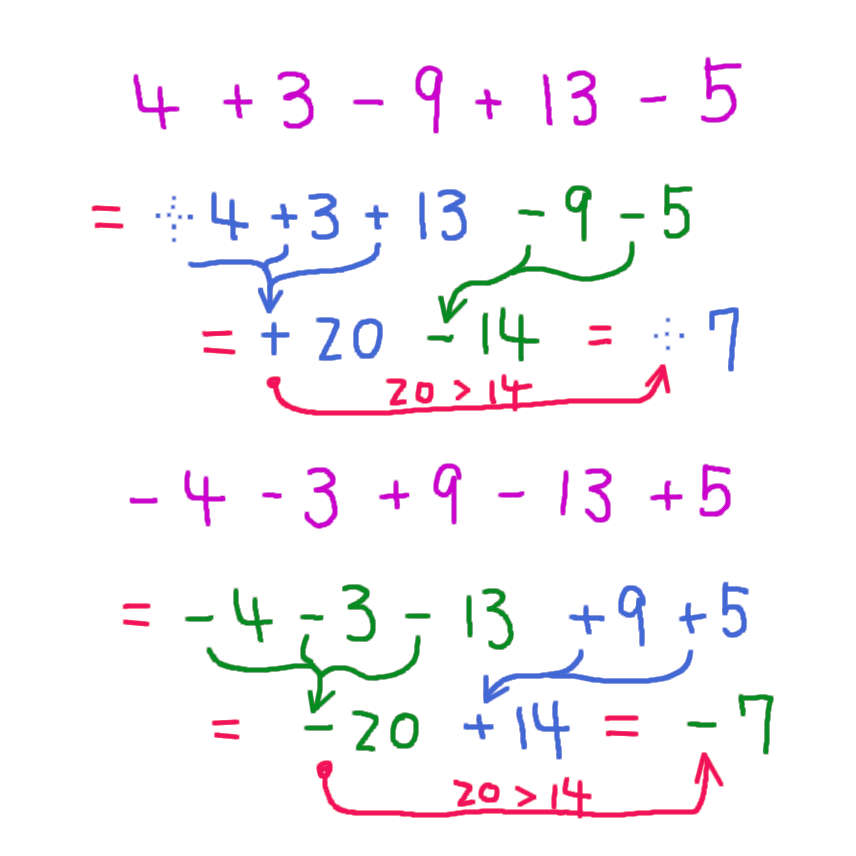
▼カッコを省略したあとの方法は
-
同じ符号 ⇒ 絶対値の足し算と 同じ符号
-
異なる符号 ⇒ 絶対値の引き算と 絶対値が大きい項の符号
▼カッコを省略するため方法は
-
数式先頭の「+」は省略
-
同じ符号の組み合わせ「+ +」「- -」は ⇒「+」
-
異なる符号の組み合わせ「+ -」「- +」は ⇒「-」
この5つのルールを覚えれば、正負の数の足し算引き算が できるようになります。
ところで
-
同じ符号の組み合わせ「+ +」「- -」は ⇒「+」
-
異なる符号の組み合わせ「+ -」「- +」は ⇒「-」
この2つのルールは、負の数「-」を含むかけ算の仕組みに由来しています。数直線を使って解説されることも多いですが、本質的なことは 負の数を含むかけ算の仕組みに 含まれています。
(ソモソモ論 ものすごーく頭の良い先人が 考えた仕組みの集大成が 数学という学問です。ものすごーく頭の良い誰かが 考えに考えて決めた人為的で演繹的な仕組みが数学です。誰かが そうだと決めたから ルールが決まっています。)

中学校の数学が よく分からなくなってきたとき、まず最初に 正負の数の四則演算を復習してほしいです。
2021年 令和3年 神奈川県 高校入試 数学 過去問 解説 ⇒ 2021年度 神奈川県公立高校入試問題 数学 過去問の解説
2020年 令和2年 神奈川県 高校入試 数学 過去問 解説 ⇒ 2020年度 神奈川県公立高校入試問題 数学 過去問の解説