中学校で最初に習う 正負の数の計算方法は かけ算(乗法 乗算)から覚えると 分かりやすく理解できます。

- 負の数が 偶数個 ⇒ 正の数
- 負の数が 奇数個 ⇒ 負の数
正負の数の計算は 足し算も引き算も かけ算も割り算も、このルールだけ覚えれば 解けるようになります。カッコも外せます。
負の数(マイナスの数)が 偶数個(0 2 4 6...)ならば、答えは正の数(プラスの数)になります。
負の数(マイナスの数)が 奇数個(1 3 5 7...)ならば、答えは負の数(マイナスの数)になります。
正負の数の計算方法 かけ算 乗算 乗法
まずは かけ算から覚えます。学校や教科書では 足し算引き算と カッコの外し方から習いますが、まずは かけ算(と割り算)を覚えると 全部が簡単になるはずです。

○ × ○ = 答え
かけ算(乗算)の式は こんな形をしています。○に適当な数を入れてみると「3 × 4 = 12」と計算できます。
この「○」の中に「負の数」が 何個入っているのか?に着目します。「3 × 4 = 12」の場合は「3」も「4」も「正の数」なので「負の数」は「0個」です。「0」は 偶数です。
- 負の数が 偶数個 ⇒ 正の数
- 負の数が 奇数個 ⇒ 負の数
負の数(マイナスの数)が 偶数個ならば 答えは正の数(プラスの数)になります。なので「3 × 4」の答えは 正の数の「12」になります。

-3 × 4 = -12
こちらも確認します。
「 ○ × ○ 」の中に 負の数は「-3」だけなので 負の数は「1個」入っています。「1」は奇数なので 答えは負の数(マイナスの数)になります。
- 負の数が 偶数個 ⇒ 正の数
- 負の数が 奇数個 ⇒ 負の数
負の数の個数が 奇数個なので 「-3 × 4」の答えは 負の数「-12」となります。覚えるルールは たったのこれだけです。まずはかけ算(と割り算)から練習すると コツがつかみやすいはずです。

○ × ○ × ○ × ○ = 答え
のように かける数が どんどん増えても かけ算(と割り算)は 同じルールで解くことができます。
(-2)×(-3)× 4 = 24
負の数は「-2」と「-3」の「2個」で 「2」は偶数です。負の数が偶数個ならば 答えは正の数「24」になります。
(-2)×(-3)× 5 ×(-4)= -120
負の数は「-2」「-3」「-4」の「3個」で 「3」は奇数です。負の数が奇数個ならば 答えは負の数「-120」になります。

もう1度まとめます。
- 負の数が 偶数個 ⇒ 正の数
- 負の数が 奇数個 ⇒ 負の数
このルールだけで 正負の数の割り算(除算 除法)も解けるようになります。

かけ算 割り算が 入り混じっていても 正負の数の計算は 同じ仕組みで解くことができます。
-3 × 5 ÷(-2)×(-8)= -60
負の数は「-3」と「-2」と「-8」の「3個」で 「3」は奇数です。負の数が奇数個ならば 答えは負の数「-60」になります。
正負の数の計算方法 足し算 引き算 加法 減法
次に 正負の数の 足し算と引き算を練習します。といっても 小学校のときに考えていた「足し算」と「引き算」とは まったく!違います。
「足し算」「引き算」ではなくて ⇒ 「+」と「-」の戦いです。
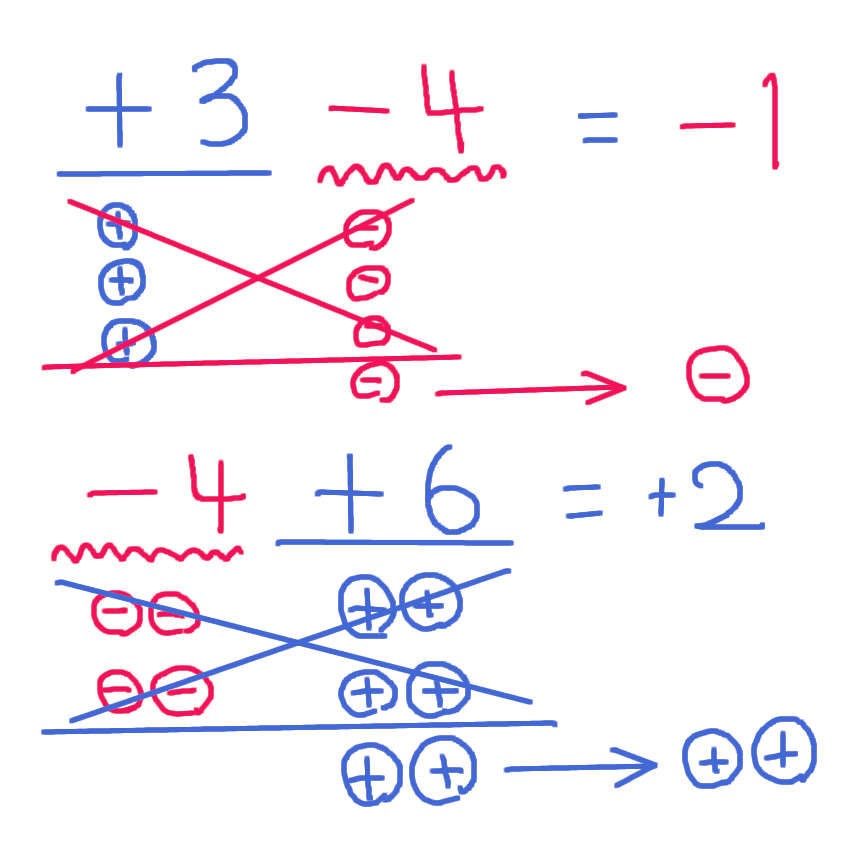
+3 -4 = -1
「+3」と「-4」が ならんだとき
「+3」は「+」が「3個」ある状態。
「-4」は「-」が「4個」ある状態。
と考えます。
「+」と「-」は 戦うと 打ち消しあいます。「+」と「-」で 個数が多いほうが 個数が多い分だけ 勝ち残ります。
「+3」と「-4」が ならんだとき 「-」のほうが「1個」多いので 「-」が「1個」勝ち残ります。
なので
+3 -4 = -1
となります。
小学校で習った 足し算と引き算とは まったく違います。「足し算」「引き算」ではなくて ⇒ 「+」と「-」の 個数の戦いです。
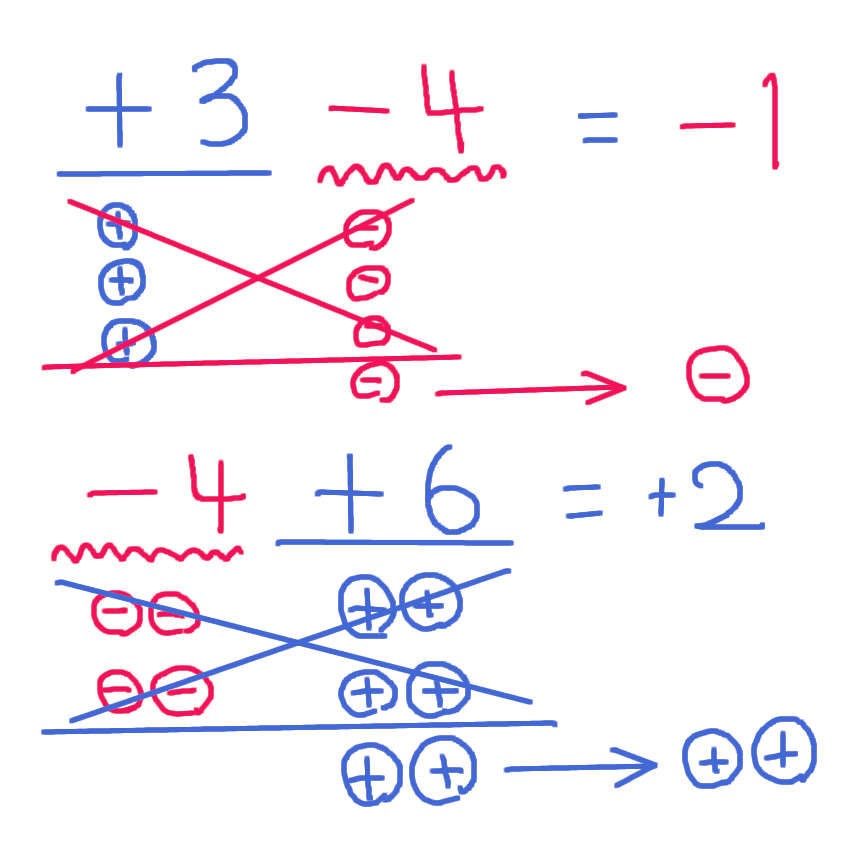
-4 +6 = +2
「-4」と「+6」が ならんだとき
「-4」は「-」が「4個」ある状態。
「+6」は「+」が「6個」ある状態。
と考えます。
「+」と「-」は 戦うと 打ち消しあいます。「+」と「-」で 個数が多いほうが 個数が多い分だけ 勝ち残ります。
「-4」と「+6」が ならんだとき 「+」のほうが「2個」多いので 「+」が「2個」勝ち残ります。
なので
-4 +6 = +2
となります。
小学校で習った 足し算と引き算は 中学生になったら 忘れてください。「+」の数 と「-」の数で どっちの数が多いのか。勝ち残った者が 答えになります。

3 -4 -7 +5 = -3
このように 項が増えた場合は 「+」のグループと 「-」のグループに 集まってもらってから 勝負します。
「+」のグループは「+3」と「+5」です。
「-」のグループは「-4」と「-7」です。
「+」のグループは 集めると「+8」になります。「-」のグループは 集めると「-11」になります。
ここまでくれば さっきと同じように 解くことができます。
+8 -11= -3
「+8」と「-11」が ならんだとき
「+8」は「+」が「8個」ある状態。
「-11」は「-」が「11個」ある状態。
と考えます。
「+」と「-」は 戦うと 打ち消しあいます。「+」と「-」で 個数が多いほうが 個数が多い分だけ 勝ち残ります。
「+8」と「-11」が ならんだとき 「-」のほうが「3個」多いので 「-」が「3個」勝ち残ります。
なので
+8 -11= -3
となります。

このように「+」グループと「-」グループが 式の中で バラバラの場合は、まずはひとつに集めてから 正負の数(「+」と「-」)の 個数の戦いを進めます。
正負の計算 カッコの外し方
いよいよ本題です。中学校では 一番最初に習う 正負の数の カッコの外し方です。

その前に まずは これを思い出してください。
- マイナス(負の数)が 偶数個 ⇒ 正の数
- マイナス(負の数)が 奇数個 ⇒ 負の数
このルールさえ 覚えていれば カッコの外し方も 簡単です。

3 +(-4)= -1
計算記号の「+」と 正負の符号の「-」が連続し「+ -」になっています。「+ -」の中の「-」は「1個」です。 「1」は奇数なので「+(-4)」は 負の数「-4」に変換しカッコを外します。
3 +(-4)= 3 -4 = -1
このように カッコを外して計算します。
- マイナス(負の数)が 奇数個 ⇒ 負の数
「+ -」のように「-」が「1個」⇒「奇数」の場合は 負の数に変換して カッコを外します。

-4 -(+2)= -6
計算記号の「-」と 正負の符号の「+」が連続し「- +」のようになっています。「- +」の中の「-」は「1個」です。 「1」は奇数なので「-(+2)」は 負の数「-2」に変換しカッコを外します。
-4 -(+2)= -4 -2 = -6
このように カッコを外して計算します。

-4 -(-2)= -2
計算記号の「-」と 正負の符号の「-」が連続し「- -」のようになっています。「- -」の中の「-」は「2個」です。 「2」は偶数なので「-(-2)」は 正の数「+2」に変換しカッコを外します。
-4 -(-2)= -4 +2 = -2
このように カッコを外して計算します。
- マイナス(負の数)が 偶数個 ⇒ 正の数
「- -」のように「-」が「2個」⇒「偶数」の場合は 正の数に変換して カッコを外します。
もうちょっと続けます。

-3 -(-5)= +2
計算記号の「-」と 正負の符号の「-」が連続し「- -」のようになっています。「- -」の中の「-」は「2個」です。 「2」は偶数なので「-(-5)」は 正の数「+5」に変換しカッコを外します。
-3 -(-5)= -3 +5 = +2
このように カッコを外して計算します。
- マイナス(負の数)が 偶数個 ⇒ 正の数
- マイナス(負の数)が 奇数個 ⇒ 負の数
このルールを覚えていれば 正負の数の かけ算も割り算も 足し算も引き算も解くことができて カッコも外せます。
正負の数の計算の 覚え方 教え方 考え方
なぜか。
- マイナス(負の数)が 偶数個 ⇒ 正の数
- マイナス(負の数)が 奇数個 ⇒ 負の数
正負の数の かけ算と割り算を 解くためのルールだけで、なぜカッコを外すことができるのかを ちょっとだけ書きます。

「-(-5)」は かみくだいて書き示すと「-1 ×(-5)」を 表しています。
-1 ×(-5) = +5
負の数は「-1」と「-5」の「2個」で 「2」は偶数です。負の数が偶数個ならば 答えは正の数「+5」となります。
よって「-(-5)」は「+5」に変換し カッコを外すことができるのです。
もう1例。

「+(-4)」は かみくだいて書き示すと「+1 ×(-4)」を 表しています。
+1 ×(-4)= -4
負の数は「-4」だけの「1個」で 「1」は奇数です。負の数が奇数個ならば 答えは負の数「-4」となります。
よって「+(-4)」は「-4」に変換し カッコを外すことができるのです。
- 負の数が 偶数個 ⇒ 正の数
- 負の数が 奇数個 ⇒ 負の数
カッコの外し方を考えると 結局 このルールに 戻ってきます。だから このルールだけ覚えて使いこなせれば、正負の数の 足し算も引き算も かけ算も割り算もできるし カッコも外せるようになります。

ということは
正負の数の計算を勉強するときに 足し算引き算(加法減法)のルールを理解するためには、かけ算割り算(乗法除法)のルールを先に知っている必要が あるのです。
なので
正負の計算を勉強するときには、かけ算割り算から勉強して覚えると いいかと思います。
(中学校の数学の教科書に載っている順番とは 少し違うので こっそりとお勉強してください)
中学生にも読んでほしい割合の問題の解き方 ⇒ 公式を使わない 割合の問題の解き方