割合の問題は「何倍?」に置き換えて考えると ちょっとだけ分かりやすくなります。

8は 4の2倍です。
8 = 4 × 2
4 × 2 = 8
「まるまるは ほにゃららの 何倍です」という文章は、小学校3年生くらいから 教科書によく出てくる表現です。
ですので、(割合を学習する)小学校5年生には 親しみやすく 理解しやすい文章かと 思われます。
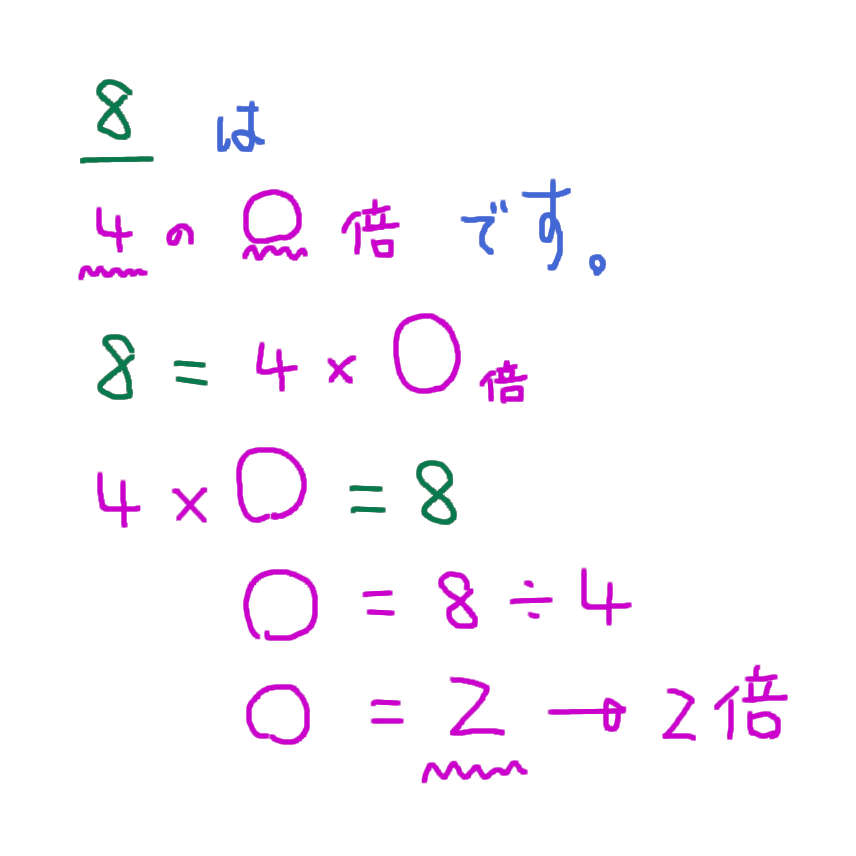
このように「何倍です」の部分が分からないときは、「4 × 2 = 8」のような 簡単な数の式を考えることで「4 × ○ = 8」のように(文章と同じ意味を表す)正しい式を組み立てることができます。
○ = 8 ÷ 4
○ = 2
なので「8は 4の2倍」と求めることができます。
割合は「何倍?」と 同じ意味
「割合」と「何倍?」は 同じ意味です。(ちょっと強引な表現ですが)

ブタは ネコの2倍です。ブタが 8ぴきのとき、ネコは 何ひきですか?
さっきの 8 = 4 × 2と同じように文章を読むことで「ブタ = ネコ × 2」という式を作ることができます。
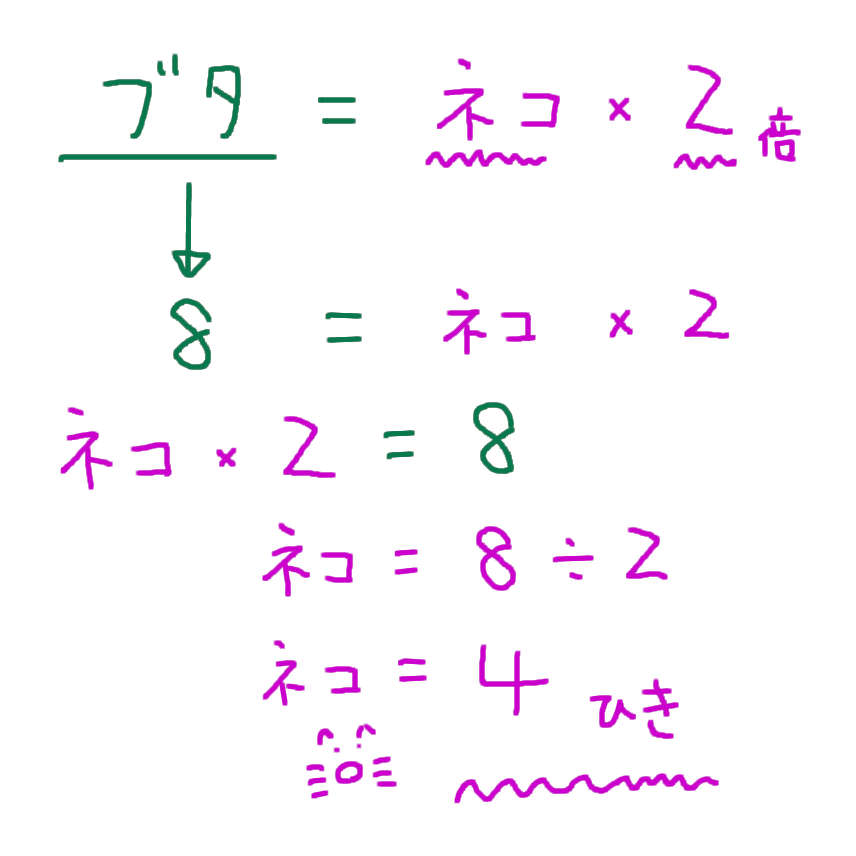
「ブタ = ネコ × 2」なので、ブタが8ぴきという情報を式に入れこむと「8 = ネコ × 2」となります。
8 = ○ × 2
○ × 2 = 8
○ = 8 ÷ 2 = 4
このように計算をすすめると「ネコは 4ひき」と 答えを求めることができます。この問題(何倍の問題)が解けるのならば、割合の問題も 同じように 解くことができます。

「割合」は「何倍」と同じ意味です。
6割 ⇒ 0.6倍
「6割」は「0.6倍」と同じ意味を表しています。
「大人のブタ = ブタ全体 × 0.6」
「何倍?」の問題と同じように文章を読めば、「大人のブタ」と「ブタ全体」の割合関係式を作ることができます。

「大人のブタ = ブタ全体 × 0.6」なので、ブタ全体が40ぴきという情報を式に入れこむと「大人のブタ = 40 × 0.6」となります。
大人のブタ = 40 × 0.6
大人のブタ = 40 × 0.6 = 24
このように計算を進めることで「大人のブタは24ひき」と 答えを求めることができます。「何倍の問題」と 同じような考え方で「割合の問題」も 解くことができました。
公式を使わない 割合の問題の解き方
くもわ(公式)や、比べる量 もとにする量(比べられる量 全体の量)などの難しい言葉を 使わなくても、「何倍?」を考えると 割合の問題を解くことができます。

「何倍?」の問題と同じように文章を読んで、「大人のブタ」と「ブタ全体」の関係式を作ります。
「大人のブタ = ブタ全体 × 何倍?」

「大人のブタ = ブタ全体 × 何倍?」という関係式に「ブタ全体が40ぴき」と「大人のブタが10ぴき」という情報を代入して「10 = 40 × ○」とします。
大人のブタ = ブタ全体 × 何倍?
10 = 40 × ○
40 × ○ = 10
○ = 10 ÷ 40
○ = 0.25
0.25倍 ⇒ 25% もしくは 2割5分
「0.25倍」は「25%」もしくは「2割5分」と同じ意味になります。
このように計算を進めることで「大人のブタは ブタ全体の25%」と 答えを求めることができます。
これもやっぱり「何倍の問題」と 同じような考え方で 解くことができました。

以下 ちょっと むむむ な お話。
割合の単元が始まると「くらべる量」とか「くらべられる量」とか「もとにする量」などの言葉が 突然!教科書に出現します。
そして 多くのお子様は どれが「くらべる量」で どれが「くらべられる量」なのか 分からなくなります。
(どっちを どっちで 割っていいのか分からなくなります。)
なんですけど
よく考えてみると「くらべる量」も「くらべられる量」も、「何倍ですか?」の単元を習ったときに 知らぬ間に 気がつかぬうちに 学習済みのはずです。
「割合」と「何倍?」は 似たような意味を表しています。もし割合の問題が 上手に解けなくて困っている場合は、「何倍?」の問題に立ち戻って考えると、ヒントに気がつけるかもしれません。

何倍の問題を 読解する ⇒ 苦手な文章題を解くヒント